贾宪三角

 开方作法本源(杨辉注：出释锁算书^①,贾宪用此术。)

 增乘方求廉法草曰(原注：释锁求廉本源):列所开方数(原注：如前，五乘方列五位，隅算在外。)以隅算一，自下增入前位，至首位而止。(原注：首位得六，第二位得五，第三位得四，第四位得三，下一位得二。)复以隅算如前升增，递低一位求之。

 

宋·杨辉《详解九章算法》引贾宪说(《永乐大典》卷一六三四四)

 [注]①此为一书名，抑或指讨论开方的数学书，书简有缺，不可得而定。
 【评】开方作法本源系贾宪首创，今称贾宪三角，西方十七世纪出现的巴斯加三角与此相同。其每一行都是某次幂的二项展开式的系数。增乘方求廉法给出了求各项系数的一般程序，由此可知，贾宪已能求出任意层数的贾宪三角，能开任意高次的方，而且，求廉的增乘方法即随乘随加方法开辟了开方运算的新蹊径。实际上，在中国数学史上，贾宪三角的主要意义不在于开方，而在于垛积。元朱世杰《四元玉鉴》的“古法七乘方图”,用两组分别平行于左斜、右斜的直线将1,1,1,1,……;1,2,3,4,……;1,3,6,10,……;1,4,10,20,……;……连结起来，这些数列恰恰是朱氏所解决的各种垛积的各项，说明朱氏各种垛积公式即高阶等差级数求和问题的解决与贾宪三角有密切关系。在此基础上，清数学家项名达、李善兰等又创造了各种数字三角形，都可以称为增广贾宪三角，清代数学家借此解决了各种更为复杂的垛积问题。

064 贾宪三角

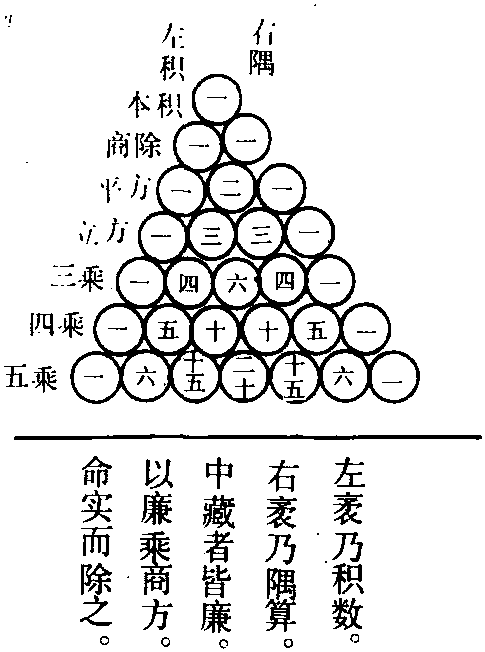
开方作法本源图之今称。它是指数为正整数的二项展开式的系数构成的三角形数表 (见图)。西方称之为帕斯卡(B. pascal,1623-1662)三角形，但11世纪上半叶贾宪在其所著《释锁》中已首先提出，早于西方600多年。《释锁》已失传。南宋杨辉所撰《详解九章算法》载有此图，并自注：“出《释锁》算书，贾宪用此术。”使这一重要成就得以流传至今。贾宪三角最初是用来开方的，故称“开方作法本源图”。数表下的注文中“左袤乃积数，右袤乃隅算。中藏者皆廉”，讲其结构与在开方术中的作用。“积”、“隅”、“廉”分别指二项展开式中aⁿ、bⁿ与中间各项的系数。“以廉乘商方，命实而除之。”讲用各行系数随乘随加进行开方的方法。对于任意n∈N，表中横向第n+1行是 (a+b)ⁿ展式各项系数，斜向第n+1行构成n阶等差数列。贾宪三角在数学的许多领域都有重要应用。可用来展开以任意正整数为指数的二项式； 直接作任意高次幂的开方，其过程比《九章算术》中传统的开方方法简便得多。进而开辟了求高次方程的数值解的新途径——增乘开方法。亦可用于高阶等差数列求和。对于宋元及其以后数学的高度发展有重要的开创性的奠基作用。是数学史上的重大发现之一。