福利经济学第一定理和第二定理first theorem and second theorem of welfere economics

从数学上说明帕累托优效配置和竞争均衡的关系。在阿罗—德布鲁一般均衡模型中，一个消费—产出向量组{x₁，…，x₁;y₁，…，y_m}如满足总需求等于总供给，即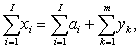则称此向量组为一个可行的配置，简记为{x;y}。
对一个可行的配置(x;y)，如果不存在别的可行配置(x′;y′)，使得

x′_i≳x_i(或u_i(x′_i)≧u_i(x_i)) i=1，…，I

且
x′_j>x_j(或u_j(x′_j)>U_j(x_j))，对某一个j则称(x;y)为一个帕累托优效配置(Pareto efficient allocation)。
福利经济学第一定理。 如果{;₁，…，₁;ŷ₁，…，ŷ_m}是一个竞争均衡，则{₁，…，₁;ŷ₁，…，ŷ_m}必是一个帕累托优效配置。
这个定理说明竞争均衡的最优性。
福利经济学第二定理。如果{x^*;y^*}是一个帕累托优效配置，且x_i^*>0(i=1，…，I)。则当每个消费单位的偏好关系是凸的、连续的和严格单调的，且每个生产单位的生产可能性集合是凸的时候，必存在一个非负价格向量≧0，使得{;x^*;y^*}组成一个竞争均衡。