混合策略

博弈论中，策略的一种类型。规定参与者在每一种给定的信息下，以某种概率分布随机地选择不同行动的策略。

混合策略mixed strategy

是纯策略的某种加权组合，权数表达了选择纯策略的概率。
设有一含N个局中人的对策，S_i是局中人i(=1,2，…，N)的纯策略集。形式上，称任何满足：

的函数σ_i:S_i→[0,1]为局中人i的一个混合策略，其中σ_i(s_i)解释为i选择策略s_i的概率。
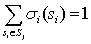
引入混合策略概念的主要好处在于它使得纳什均衡必定存在。考虑如图所示的标准型对策，它不存在纯策略纳什均衡。记σ_A（上）=τ,σ_B（左）=λ,0≤τ,λ≤1。混合策略组或行动σ=(σ_A,σ_B)完全决定于τ,λ，就简记为(τ,λ)。在(τ,λ)之下，局中人i的期望支付为

Eu_i(τ,λ)=τ[λu_i(上，左)+(1-λ)u_i(上，右)]+(1-τ)[λu_i(下，左)+(1-λ)u(下，右)]

其中i=A,B。若一个行动()同时满足以下两个不等式：

Eu_A()≥Eu_A(τ,)，对所有0≤τ≤1,
Eu_B()≥Eu_B(,λ)，对所有0≤λ≤1,

则称()为一个混合策略纳什均衡。

以支付矩阵的数据代入，得Eu_A(τ,λ)=(1-τ)(2λ-1),Eu_B(τ,λ)=(1-λ)(3-4τ)。容易验证，当＝3/4,＝1/2时，上述两不等式同时成立，因此行动(3/4,1/2)是一个混合策略的纳什均衡。

混合策略

参与对策的局中人以一定的概率值随机地选取的策略。它可以用向量形式进行表述。在矩阵对策中，它只有在没有鞍点的情况下才出现。因为在矩阵对策中没有鞍点时，参与对策的局中人无法有目的地选取对策来求得平衡局势，只有随机地从策略集合中选取策略。