极限思想jixian sixiang

略述如下：一个变量u，它取一连串的某个确定的数量A的近似值，这一连串的值越来越逼近A，通过对这一连串近似值的考察将A唯一地确定下来.即任意给定正数ε，当u变化到一定时刻，可使这时刻以后的u值与A的差|u-A|小于此正数ε.
极限思想在中国和外国很早就产生了，经过许多世纪的顽强探索，特别是当世界进入了资本主义社会，由于生产力、科学技术发展的强有力推动，极限思想才发展起来.公元17世纪时数学家将许多问题归结为两类.第一类是在非匀速运动中求某一瞬时的速度问题，或与之本质上相同的，求曲线上的切线问题，更广泛的说，是求函数的变化率问题.第二类是求曲线所包围的面积问题，或与之本质相同的，在非匀速运动中求所经过的路程问题.这两类问题分别导致微分学与积分学的产生.而导数和积分概念又都建立在极限概念的基础上.
在牛顿和莱布尼兹总结前人工作开始创立微积分的时候，极限概念还是模糊的.因此受到了贝克莱主教的强烈攻击，造成了数学历史上的第二次危机，后来经过柯西、维尔斯特拉斯等许多数学家的努力，才给出了极限概念的精确定义.
现在将目前使用的精确定义极限概念的“ε-N”，“ε-δ”方法叙述如下：
定义：若{u_n}为一实数数列，A为一实数，任意给定一个正数ε，存在正整数N，使当n取大于N的一切整数值时，都有|u_n-A|<ε(或u_n与A在实数轴上的距离p(u_n,A)<ε；或u_n∈0 (A,ε)即u_n点落在以A为中心以ε为半径的区间(A-ε,A+ε)中)则称当n趋向于∞时，数列{u_n}有极限A.以符号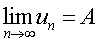表示.
定义：对于实变量函数f(x),x₀及A为一实数，任意给定一个正数ε，存在正数δ，当x取值满足0<|x-x₀|<δ时，有|f(x)-A|<ε.则称当x→x0时，函数f(x)以A为极限.用符号f(x)=A表示.