无理数指数幂
无理数指数幂wulishu zhishumi
假设a是一个任意的正数,a是一个任意的正无理数,那么aa叫做无理数指数幂.并规定:aa是存在于以a为底,以a的不足近似值为指数与过剩近似值为指数的幂的数列之间,并等于这两个数列的共同的极限.
例如,设a= 10,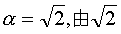 的精确到0.1,0.01,0.001,…1/10n,…的不足近似值和过剩近似值,给出两个数列
的精确到0.1,0.01,0.001,…1/10n,…的不足近似值和过剩近似值,给出两个数列
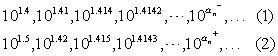
因为当底数大于1时,指数越大,这个幂的值也越大,所以数列(1)是递增数列,并且总小于101.5;同样数列(2)是递减数列,并且总大于101.4,即数列(1) (2)均是单调有界数列,故均有极限.因为
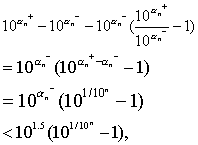
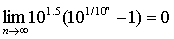
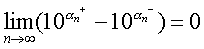
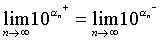
这就证明了数列(1)和(2)有共同的极限.这个极限是存在且唯一的.用
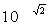
表示这个极限,即
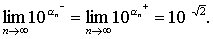
同时规定:a-a=1/aa(a> 0,a是正无理数).
零的正无理数次幂规定为零,零的负无理数次幂没有意义.例如
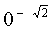 无意义(零不能作除数).
无意义(零不能作除数).无理数指数幂的定义,在底数是负数时没有意义.例如,要确定
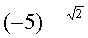 的意义,需要用(-5)1.4,(-5)1.41,…来做它的近似值,但是分数指数幂在底数是负数时没有意义.
的意义,需要用(-5)1.4,(-5)1.41,…来做它的近似值,但是分数指数幂在底数是负数时没有意义.可以验证,有理指数幂的运算法则对于任意无理数指数幂仍能够适用.
☚ 有理数指数幂的运算法则 实数指数幂 ☛
- 吉尔是什么意思
- 吉尔·布拉斯是什么意思
- 吉尔·布拉斯是什么意思
- 吉尔·布拉斯是什么意思
- 吉尔伯特是什么意思
- 吉尔伯特群岛是什么意思
- 吉尔伯特,威是什么意思
- 吉尔伯特,汉是什么意思
- 吉尔伽美什是什么意思
- 吉尔伽美什是什么意思
- 吉尔伽美什是什么意思
- 吉尔伽美什是什么意思
- 吉尔伽美什与阿伽是什么意思
- 吉尔伽美什史诗是什么意思
- 吉尔利-卡米斯法是什么意思
- 吉尔加克人是什么意思
- 吉尔加克人是什么意思
- 吉尔努斯是什么意思
- 吉尔博亚是什么意思
- 吉尔古德,约翰,爵士是什么意思
- 吉尔吉斯人(Киргизы)是什么意思
- 吉尔吉斯作家协会是什么意思
- 吉尔吉斯斯坦是什么意思
- 吉尔吉斯斯坦农业政策改革立法是什么意思
- 吉尔巴特,詹姆斯·威廉是什么意思
- 吉尔布雷思是什么意思
- 吉尔布雷思是什么意思
- 吉尔布雷思是什么意思
- 吉尔布雷思是什么意思
- 吉尔布雷思夫妇是什么意思
- 吉尔布雷思夫妇是什么意思
- 吉尔布雷斯是什么意思
- 吉尔德斯利夫是什么意思
- 吉尔德斯布利是什么意思
- 吉尔摩是什么意思
- 吉尔摩尔是什么意思
- 吉尔斯台兹是什么意思
- 吉尔斯台兹是什么意思
- 吉尔施是什么意思
- 吉尔曼是什么意思
- 吉尔杭阿是什么意思
- 吉尔杭阿是什么意思
- 吉尔杭阿是什么意思
- 吉尔杭阿是什么意思
- 吉尔杭阿是什么意思
- 吉尔杭阿(?—1856)是什么意思
- 吉尔松是什么意思
- 吉尔松是什么意思
- 吉尔松是什么意思
- 吉尔波丁是什么意思
- 吉尔洪额是什么意思
- 吉尔焦莫尔约是什么意思
- 吉尔特勒是什么意思
- 吉尔福特是什么意思
- 吉尔福特是什么意思
- 吉尔福特是什么意思
- 吉尔福特智力三维结构模型是什么意思
- 吉尔罗伊是什么意思
- 吉尔耶是什么意思
- 吉尔贝里是什么意思