数学符号Shuxue fuhao

有一定数学含义的专用标记。在数学发展中， 数学符号起着极为重要的作用。不论对数学的整体还是对它的任何一个分支，选用一套适宜的符号都是必需的， 这不仅有助于提高思考与计算的效率，有助于揭示数学的内在规律，推广已有成果，启发思维，还有助于缩短学习时间，使人们更快地领会有关问题的实质。形成今天通用的一整套数学符号，经历了漫长的历史时期。虽然作为一门理论科学的数学已经存在了2 000多年， 但在数学中普遍使用符号却只有400年左右的时间。
现代数学符号主要是欧洲文艺复兴时期以来创造的， 其来源大致有以下几种：
❶文字的缩写。如： π 取 自 希腊文圆周(περιφερια) 的字头；d （直径）、i （虚数单位） 都是相应的拉丁文单字的字头；Log（对数）、sin（正弦）、Lim（极限）,mod（模）则是相应拉丁文或英文单字的头几个字母。

❷象形。如平行：∥；垂直：丄； 三角形：△；圆：⊙。

❸会意。如： 等号： =; 大于、小于： >、<; 括号： ()、〔 〕； 除号： ÷。

❹人为规定。如：加号、减号：+、-; 自然对数的底e; 非负整数n的阶乘n! 等。
在各种数学符号中， 最基本的莫过于四则运算符号、等号、大于及小于符号、括号和表示未知数的符号了， 这里简略叙述其历史发展。
加号与减号。巴比伦、埃及、希腊的加法一般都不用专门的记号，尤其后两者的数字不是位值制的，加法基本上是用积累的方式完成， 对于加号更无明显的需要，但埃及人有时用表示 “走来”的符号Λ表示相加，用表示“走去”的符号Λ表示相减。他们有时也用水平方向的三个箭头表示两数之差。巴比伦人用 表示相减，40—13被写作。希腊人用倒写的希腊字母ψ表示相减， 即 “↑” 或 “↑”。在海伦(Heron)和丢番图的著作中多次使用过它们。在中国古代，简单的加减法运算也不用符号，但为了区分正数与负数，曾使用不同颜色的算等，后来在表示方程各项系数时，对于负数在相应的筹码上加一根斜放的筹（划一斜线），它实际上起着减号的作用。由于方程的各项是用分离系数法表示的， 对于正项一般不必使用单独的加法记号。15世纪末至16世纪，意大利人用或P(拉丁文 “相加”的字头)表示加，用或m(拉丁文“相减”的字头)表示减。同一时期在欧洲也流行用拉丁文et（和）表示加，有一种说法是由 “e”演变成了后来的“十”号。15世纪后期，德国人开始用 “+”和“-”分别表示加和减。据说最初这是码头上表示箱子超过与不足标准重量的记号。1489年，捷克人维德曼(Widman, J)在他于1489年出版的《简算和速算》一书中正式用+、-作为加、减号，这是它们首次在印刷本图书中被这样使用。但直到16世纪后期它们才流行起来。1626年， 法国人吉拉尔 (Girard, A.) 用ou表示 “加或减”， 1631年， 英国人奥特雷德OughtredW.单独用±表示加或减。
乘号与除号。埃及、希腊、中国和印度都没有引入表示乘法的专门记号。巴比伦人使用了一个十分繁琐除法是使用倒数表化为乘法进行的， 因此不必引入除号。在古希腊， 除法是直接用相应的希腊文单词表示的。16世纪， 德国数学家施蒂费尔 (Stifel, M.,) 在其著作中用大写字母M (拉丁文 “乘法”的第一个字母)表示乘，用D(拉丁文“除法”的第一个字母)表示除。稍后，荷兰人斯台文也用了这种记号，法国数学家韦达用“AinB”表示A×B, 同时代也有人用“via”表示乘。“×”最初在1478年出版的意大利特雷维索(Treriso) 算术中被用作交叉相乘的记号， 书中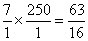
表示 (1×250×63) ÷ (7×1×16), 16世纪许多数学书中也用×作为交叉相乘的记号， 最早单独地把×用作两数相乘的记号的，是1618年出版的英国人赖特 (Wright, E., 1561—1615) 翻译的纳皮尔 《奇妙的对数定律说明书》一书的附录，一般认为这个附录是奥特雷德写的，其中说：“表示加的符号是+，减的符号是一，乘的符号的是×”。1631年，奥特雷德在他的《数学入门》中也如此使用了×号，以后它便渐渐通用。1583年， 德国数学家克拉维斯 (Clarius) 在他的《实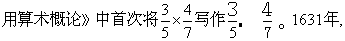英国人哈里奥特Harriot用2.aaa表示2a³。1698年，莱布尼茨在一封信中提出用“·”代替“×”表示乘，因为后者太容易与字母“x”混淆， 以后用“·”作乘号也渐渐流行。17世纪流行过多种乘法记号， 如*,☐，”，’，∫等，但只有×和·沿用下来。1544年，施蒂费尔在他的《综合算术》中用8)24和8)24(表示24÷8。1522年， 德国人里泽 (Riese, A.) 用÷表示减号，在很长时间里通行。1659年，瑞士人拉恩(Rahn,J.H.)在他的一本代数书中首次用÷作为除号。1668年他的书被译成英文，÷作为除号逐渐被广为采用。比号“：”大约起源于17世纪初，1633年出版的一本算术书中，3:4被用来表示3/4。1651年出版于伦敦的一本天文学著作中明确地用：作为比号，1684年莱布尼茨在一篇论文中把它用作一般的除法记号， 后来也较流行。
等号。古埃及人使用过几种等号。在阿默斯纸草书中，用表示相加的结果，埃及人也用表示一系列运算的结果，意为“它使得”。猫头鹰的图案也被用作等号。在希腊数学中，丢番图用1°或l′(.l6 os的缩写，原词意为相等)作为等号。现代通用的等号=是英国人雷科德 (Recorde, R.) 在他的 《智力的磨石》(1557)中引入的，他说：“再也没有别的两件东西比它们更相等了。”但此后很长时间用=表示等号并未流行，在16世纪最大的数学家，也是近代对数学符号的系统引入做出决定性贡献的韦达的著作中，=表示相减。1559年， 彪特(Butev,J., 法国) 用 “ 〔”表示相等， 1575年， 克胥兰德 (Xylander, G., 德国) 用“‖”； 1634年， 埃利贡Herigone,p.法国用2/2(或2|2)。1637年， 笛卡尔用 “=”表示现代“±”的含义， 而用∝或∝表示相等， 并且沿用到18世纪，1680年，莱布尼茨同时用=和表示相等。“=”用作等号而普遍使用已经是18世纪的事了。
大于及小于符号。1629年，吉拉尔分别用ff和§表示大于和小于，1631年，在哈里奥特去世10年之后出版的他的《实用分析术》中，首次引入>和<表示大于和小于。同一年， 奥特雷德用和表示大于和小于，1647年又用和表示不大于和不小于。1634年，埃利贡用3/2和2/3表示大于和小于， 直到18世纪，>和<符号才为人们普遍接受， 1734年， 布盖(Bouguer, p., 法国， 发明了≥和≤号。
括号的作用在于表明运算的顺序。1484年，舒凯(chuguet, N., 法国) 用在一些项下面加横线的方式
示其后的各项应先进行运算，例如帕乔利(1494)用R
卡尔达诺也采用了这种方式， 还有一些意大利数学家直接引入了现代括号的雏形。1550年左右，邦别利用〔〕表示括号， 1572年他又用“”。1556年，塔塔格利亚用了“(”（现在括号的前一半）16世纪中叶德国数学家施蒂费尔的手稿中首次使用了完整的 “ ()”号， 但没有出版， 1608年， 克拉维斯最早在印刷本数学书中使用了这一符号， 1593年， 韦达引入了 “ {}”号，1631年出版的哈里奥特的书中在需要先进行运算的各项上加，同年，奥特雷德用在有关各项两端加“：”另作为括号，1646年范·舒滕(van Schooten,F,.荷兰)把横线加在有关各项的上方， 17世纪许多数学家如莱布尼茨(1672)、牛顿(1676)都沿用了这种方式。到18世纪， 圆括号和方括号才得到普遍使用。
表示未知数的符号，古代埃及有一类“堆算”（参见该条）问题，其中用“堆”表示未知数。在仅有一个未知数时，印度人用“○”表示，为了与数0相区别，又有表示未知数的○下加一条竖线， 中国古代数学由于以文辞叙述为主， 在具体问题中是对具体的某些项目求解，长时间没有引入未知数的单独记法，到宋元时代的天元术(13世纪成熟)中，用“元”表示未知数。“未知量”一词的希腊文是αρ⍳θuos，丢番图一般用S表示未知数，并给出了未知数的正、负1—6次幂的记法。在欧洲，16世纪最流行的未知数记法有两种，一是用“未知量”一词的缩写或字头， 如赫克 (Hoecke, 荷兰) 1514年用pri, 卡尔达诺1545年用reb, 申贝尔(Schenbel，德国)1551年用ra。另一种是在未知数的系数上面或后面加数码，表示未知数的各个幂次，如邦别利1572年把4x²+4x写作·p↓/4; 斯台文1585年把2x+4写作2❶+4; 罗曼努斯(RomanusA.，荷兰)1593年把x⁴⁵写作1(45)；卡塔尔迪(Cataldi,P.A.，意大利)1610年把5x³·8x⁴＝40x⁷写作5384 fa407;1619年，比尔吉把8x⁶+12x⁵-9x⁴+10x³+3x²+7x-4写作。此外，还有一些数学家引入了一些较为特殊的记号 （其中有的也来源于单词的缩写或字头）, 如施蒂费尔1544年用x表示未知数；彪特1559年用ρ，等等，16世纪末至17世纪初，韦达引入了用拉丁文的元音字母作未知数， 用辅音字母作已知数的方式； 1637年，笛卡尔开始用字母表中的最后几个字母x、y、z等表示未知数（变量）, 而用开头的一些字母a、b、c等表示已知数（常量）, 后来为人们普遍使用。