广义矩法GMM

广义矩估计法是参数估计的一种方法，是普通矩估计法的推广。参数的矩估计就是用样本矩去估计总体矩。经常使用的是用样本一阶矩去估计总体一阶矩（均值），用样本二阶中心矩去估计总体二阶中心矩（方差）。较成熟的GMM方法是由Hansen(1982)引进的，现在该方法已有较普遍的应用。
设ω_i是一个h×1的观测值向量，θ是a×1的未知参数向量，h(θ,ω_i)是一个r×1的向量函数，也就是
h(·):(R^h×R^a)→R^r,R^h×R^a表示h×a实空间。
由于ω_i是随机的，所以h(θ,ω_i)也是随机的，假定当θ为参数真实值时

E[h(θ,ω_i)]=0 (1)

即函数h满足正交条件。记

y_n＝(ω′₁，…，ω′_n)′ (2)

为样本观测值的全体集合，记

为函数h(θ,ω_i)的样本均值，g(·)是一个r维向量。GMM基本思想是选择θ，使二次型
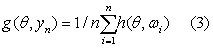
Q(θ,y_n)=[g(θ,y_n)]′W_n[g(θ,W_n)] (4)取极小值。这里权函数矩阵W_n,n=1,2，…是一个r×r的矩阵序列。
为求θ的估计值，在(4)式中取权函数矩阵W_n的初值为单位阵，即Q为普通欧氏距离，使Q取极小而得到θ_n的初值θ_n⁽¹)。将θ_n⁽¹)代入

_n＝1/ng_n(X)[h(θ_n,ω_i)][h(θ_n,ω_i)]′

(5)

可得_n⁽¹)，将_n⁽¹)代入
Q(θ,y_n)=[g(θ,y_n)]′M^-1[g(θ,y_n)] (6)(其中M是h(θ,ω_i)的样本均值g(θ,y_n)的渐进方差，M^-1是M的逆矩阵)又可得_n⁽²)，如此迭代下去，直至‖_n⁽¹)-_n⁽ⁿ)‖小于预定精度ε为止。可以证明这个迭代过程与初值无关。