平均数píngjūnshù
几个数相加所得的和除以相加数的个数所得的商。
平均数mean
反映统计研究对象某一数量标志的典型水平或代表性水平的数值。它的特点是把总体单位的数量标志值的个别差异抽象化,反映了变量值的集中趋势。平均数只能用于同类现象,并要以大量观察的资料为依据。平均数的表现形式有算术平均数、几何平均数、平方平均数、调和平均数等。
平均数pingjunshu
使用最广泛、最普通的一科集中量数。包括算术平均数、几何平均数和倒数平均数。
算术平均数 通常简称为平均数。是一群数据的总和、除以数据个数所得的商,即![]()
式中 ——算术平均数
N——数据总个数
Xi——第i个数据,i=1、2,…,N
[例1] 某小组10个学生的语文测验成绩为78、62、84、90、72、76、83、95、77、78,则其算术平均数为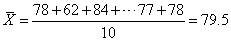
若一群数据可分成若干部分,各部分的数据个数分别为N1,N2,…,NK,各部分的算术平均数分别为1,2,…,K,则整群数据的算术平均数为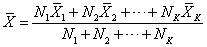
式中的N1,N2,…,NK一般是不等的,若把它们视为![]()
各部分的数据个数不同或权数不同时,要用上式来计算全体的算术平均数。
[例2] 某年级各班一次英语考试成绩如下:
| 班别 | 一 | 二 | 三 | 四 | 五 |
| 人数 | 30 | 40 | 50 | 48 | 52 |
| 平均分 | 80 | 80 | 65 | 65 | 60 |
全年级的总平均分为:
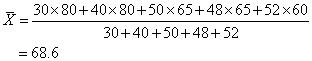
在已分组的次数分布表中,可用下式求算术平均数:
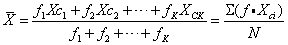 式中 f——各组的次数
式中 f——各组的次数Xci——各组的组中点,i=1,2,…,k
如根据“次数分布表”条中的数据,可计得算术平均数为
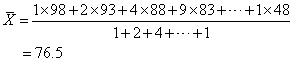
用此式计得的算术平均数与真实平均数(76.4)非常接近。
算术平均数在几何上或物理上表示一群数据的中心或重心位置。它可用于各群(组)数据之间的比较。但它易受数据中的极端值的影响,从而减弱它作为集中量数的代表性。
几何平均数 是一组数据(设有N个)连乘积的N次方根,即
若数据较多或较大时,可用取对数的方法来求几何平均数,即
几何平均数实际上是各数据对数的算术平均数,适用于计算具有递增(减)性数据的集中量数。如2、6、18、54、162为等比级数(公比为3),若求这5个数据的集中量数,则不宜用算术平均数,而应用几何平均数,因为前者(=48.4)在本数列中并不居中,而后者(G=18)恰为居中。
[例3] 1980~1983年我国职业中学的在校学生数如下。求这4年在校学生的平均数与年平均增长率。
| 年份 | 1980 | 1981 | 1982 | 1983 |
| 人数 (万人) | 13.3 | 21.3 | 35.7 | 53.9 |
显然,这是一组具有递增性的数据,故宜用几何平均数。
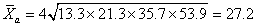
为求年平均增长率,需先求出以前一数据为基础的逐年增长率,即:21.3÷13.3=1.60,35.7÷21.3=1.68,53.9÷35.7=1.51;然后求出这三个比率的平均值,即
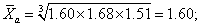
由于
还包括着以第一年的数据为基数的1,因而必须减去1,即:1.60-1=0.60。故后三年的年平均增长率约为60%。
倒数平均数 亦称调和平均数。是一组数据的倒数的算术平均数之倒数,计算公式为:
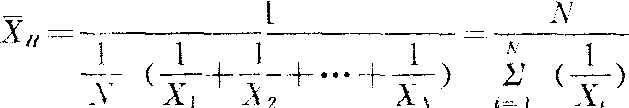
倒数平均数适用于解决平均速度一类性质的问题。
[例4] 设甲、乙、丙3个学生的解题速度如下:甲生每小时8题、乙生每小时5题、丙生每小时4题。求3人的平均解题速度?
由于此例是求平均速度问题,故应用倒数平均数。
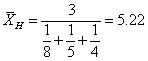
验算:由于甲生解1题所花的时间为1/8,即0.125小时、乙生所花的时间为1/5=0.2小时,丙生所花的时间为1/4=0.25小时,则他们各解1题(共解3题)所花费时间为0.575小时;根据倒数平均数,他们在0.575小时应解题数为0.575×5.22=3 (题),与事实相符。(如果是算术平均数=5.7,则在0.575小时内他们应解题数为0.575×5.7=3.3 (题),与事实不符;几何平均数
 =5.4,也与事实不符)。
=5.4,也与事实不符)。平均数Pingjunshu
使用最广泛的一种表示数据集中趋势的量数。包括算术平均数、加权平均数、几何平均数和调和平均数。算术平均数:是一组数据的总和除以数据个数所得的商。通常简称为平均数,计算公式为:
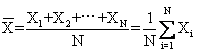
 ——算术平均数;N——数据个数;Xi——第i个数据,i=1,2,…,N。加权平均数:是一组数据中各数据与其权重之积的总和除以各权重总和所得的商,即
——算术平均数;N——数据个数;Xi——第i个数据,i=1,2,…,N。加权平均数:是一组数据中各数据与其权重之积的总和除以各权重总和所得的商,即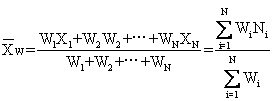
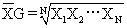
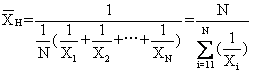
平均数
又称“平均指标”。指在同质总体内,按某一数量标志说明该总体在一定历史条件下的一般水平的综合指标。如平均人数、平均工资等。
平均数average
是同质变量的综合平均数值。用以说明这一组变量值的平均水平或集中趋势,是计算计量资料时主要的指标。平均数有算术均数、几何均数、中位数、众数和调和均数等。在医学中常用者为前三种。在实际工作中应按资料的性质和分布情况,选用适当的平均数作为代表值。
平均数
为了反映社会现象和过程在一定时间和地点条件下的典型水平,通常采用总体各单位在某一数量指标上的平均量的数。例如,不同年龄工人的平均年龄,全年各月不同月产量的月平均产量等。平均数具有高度的概括性,它把同类事物中的个别差异抽掉,显示出事物的典型特征或基本趋势。它是反映总体特征最有效的指标。其基本形式为:

但是,由于所反映事物的内容或原始资料的不同,平均数可分为简单算术平均数,加权算术平均数、调和平均数、几何平均数和移动平均数等。
简单算术平均数是若干个变量的和除以这些变量的个数所得的商。
加权算术平均数是按各个变量在总体中出现的比率或次数为权数而计算的。其通式为:
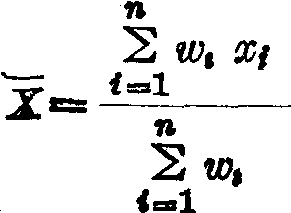
式中:——加权算术平均数;
xi——总体中第i个变量值;
wi——总体中第i个变量所占的比率或次数,即权数;
n——总体中变量的个数。
调和平均数又称倒数平均数,是变量倒数的加权算术平均数的倒数。在社会经济统计中调和平均数是在缺乏总体单位个数资料的情况下运用的。例如,已知某施工队第一小组的工人每人每日的工资为8元,共得工资总额为400元;第二小组的工人每日的工资为10元,共得工资总额为900元第三小组每人每日工资为7元,共得工资总额420元,则该施工队平均每人每日所得工资额为:
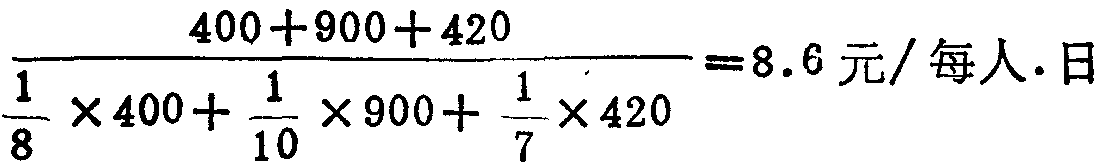
几何平均数是总体中n个变量的连乘积的n次方根。即:
![]()
移动平均数,是根据原始时间数列,及各期实际发生数,逐项移动,依次计算的平均数。其计算公式为:
![]()
式中: n——每个序时平均数所包括的序时项数;
t——每个移动平均数中末项的时期数;
yt——t时期发生的实际数据;
 ——末期为第t期的一次移动平均数。
——末期为第t期的一次移动平均数。由此可见,不同的平均数,反映了事物不同内容或不同原始资料的特征或趋势。
平均数Average
亦称“均值”,或称“平均指标”。算术平均数、几何平均数、调和平均数以及中位数、众数等的统称。但在一般情况下,专指算术平均数。平均数是数据集的中心值,代表数据的一般水平。
平均数
即统计平均指标。反映同质总体各单位在某一数量标志方面一般水平的综合指标。平均数的作用有: (1) 可以对比同类现象在不同单位、地区的一般水平;(2) 可以对比某一现象的水平在不同时间的变化,以说明这些现象的发展趋势或规律性; (3)在对现象进行分组的基础上,可以分析现象之间的依存关系。计算平均数的前提条件是社会现象的同质性,只有在同质总体内才能计算平均数。平均数的计算方法是总体的标志总量除以总体单位数。其基本公式为:
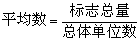
平均数
在计划统计工作中又称作平均指标。是总体各单位某方面数量的一般水平的指标,如不同工资等级职工的平均工资、某个时期某种产品产量的平均发展速度等。平均数掩盖总体各单位某方面数值上的差异,表现出总体各单位某方面数值的平均水平或趋势。平均数可以表明某种现象在一定时间地点条件下的典型特征; 可以评价不同空间和不同时间的同类现象的一般水平; 可以考察现象某方面数量在时间上的发展趋势; 可以分析总体内不同方面的数量之间的相互依存关系,如劳动生产率与工资水平之间存在着依存关系。常用的平均数有算术平均数,调和平均数和几何平均数。
计算平均数的基本方法是算术平均数,公式如下:
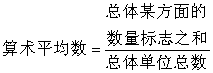
例: 某农户的小麦作物,第一块地5亩,产量2,000斤,第二块地3亩,产量1,800斤,第三块地2亩,产量1,400斤,

计算平均数时,由于所掌握的统计资料的限制,不能直接使用算术平均数方法,则要采用调和平均数方法。例如,某农户的小麦作物,第一块地亩产400斤,产量2,000斤; 第二块地亩产600斤,产量1,800斤; 第三块地亩产700斤,产量1,400斤,那么

几何平均数常用于计算某种现象的平均发展速度。
【参】 发展速度和增长速度
平均数
表明同类现象的总体内各单位所达到的一般水平或某一数量标志值的代表水平。其数值是平均数,即总体标志总量除以总体单位总数之商数。它具有两个特征:
❶用一个代表性数值说明被研究总体某种数量特征的一般水平。
❷把被研究总体某一数量标志值在总体各个单位之间的差异给抽象化了。它是一种重要的综合指标。
平均数average value
表明同类现象的总体内各单位所达到的一般水平或某一数量标志值的代表水平。其数值是平均数,即总体标志总量除以总体单位总数之商数。它具有两个特征:
❶用一个代表性数值说明被研究总体某种数量特征的一般水平。
❷把被研究总体某一数量标志值在总体各个单位之间的差异给抽象化了。它是一种重要的综合指标。
平均数
平均数是分析计量资料的基本指标,表示一组性质相同的观察值的平均水平。平均数包括算术均数、几何均数、中位数、众数及调和均数等。前三种较常用,尤其是第一种。
算术均数 简称均数,符号为X,是一组观察值的平均。均数最适用于呈正态分布的资料,其他分布资料亦可用。均数只反映数据集中的一面,对服从正态分布的资料,把均数与标准差结合起来可全面反映其分布的特征。均数有三种算法: 直接法、加权法和简捷法。
1. 直接法: 当观察值的个数不多时,可直接计算。公式为

式中∑为求和的符号,X为观察值,n为观察值的个数,一般即样本含量。
2. 加权法: 当资料有较多相同的观察值时,可用相同观察值的个数即频数f乘该观察值,以代替逐个相加。公式为
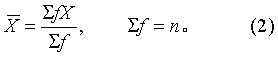
式中∑fX表示k个不同的观察值各以其频数f加权后的和: f1X1+f2X2+…+fkXk。如计算10,10,10,15,15五个观察值的均数,则
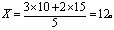
加权的涵义是指各个不同的观察值在计算均数时,由于频数不同,所起的作用也不同。频数多,权数大,作用也大;频数少,权数小,作用也小。如上面的5个观察值中,10有3个,权数为3,15有2个,权数为2。计算均数时,观察值10起3/5的作用,而观察值15只起2/5的作用。因此,均数不是10与15的平均——12.5,而是12,偏向于权数较大的10。权数相差越悬殊,这种偏向也越明显。
3. 简捷法: 适用于观察值较多并编成频数表的资料。其原理与计算步骤如下:
(1) 以各组中值代表本组段的各观察值。组中值是本组段下限与相邻较大组段下限之平均,如表1第一组段的组中值X=(370+390)/2=380,即第(3)栏数字。
(2) 将X按下式简化为缩简值x,
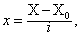
式中X0为假定均数,一般选频数较多而居中一组的组中值,如表1选X0=480;i为组距,如表1,i=20;第一组段的x=(380-480)/20=-5,余类推。假定均数所在组段x=0。通常若频数表的组距相等,则不必计算,可在组中值定为X0的组段写0,然后在0的上下,对组中值小于X0的各组段依次写-1,-2,…;对组中值大于X0的各组段依次写1,2,3,……,如表1第(4)栏。(3)求∑fx,即将各组段的频数f与x相乘,然后求和。
(4)按式(3)求均数,即对假定均数进行校正,
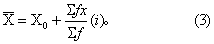
例1 某市20个男婴的出生体重(g)如下,求其平均体重。2770 2915 2795 2995 2860 2970 3087 3126 3125 46542272 3503 3418 3921 2669 4218 3707 2310 2573 3881例数不多,宜用直接法,按式(1)计算平均体重为
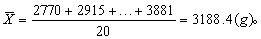
例2 1301名大骨节病妇女的初潮年龄如下,求其平均初潮年龄。
| 初潮年龄(岁) 例数 | 11 12 13 14 15 16 17 18 19 合计 19 45 133 206 284 280 203 89 42 1301 |
相同年龄者很多,宜用加权法,按式(2)计算平均初潮年龄为
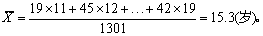
例3 求表1第(1)、(2)栏资料红细胞数的均数。
表1 130例正常成年男子红细胞数用简捷法计算均数
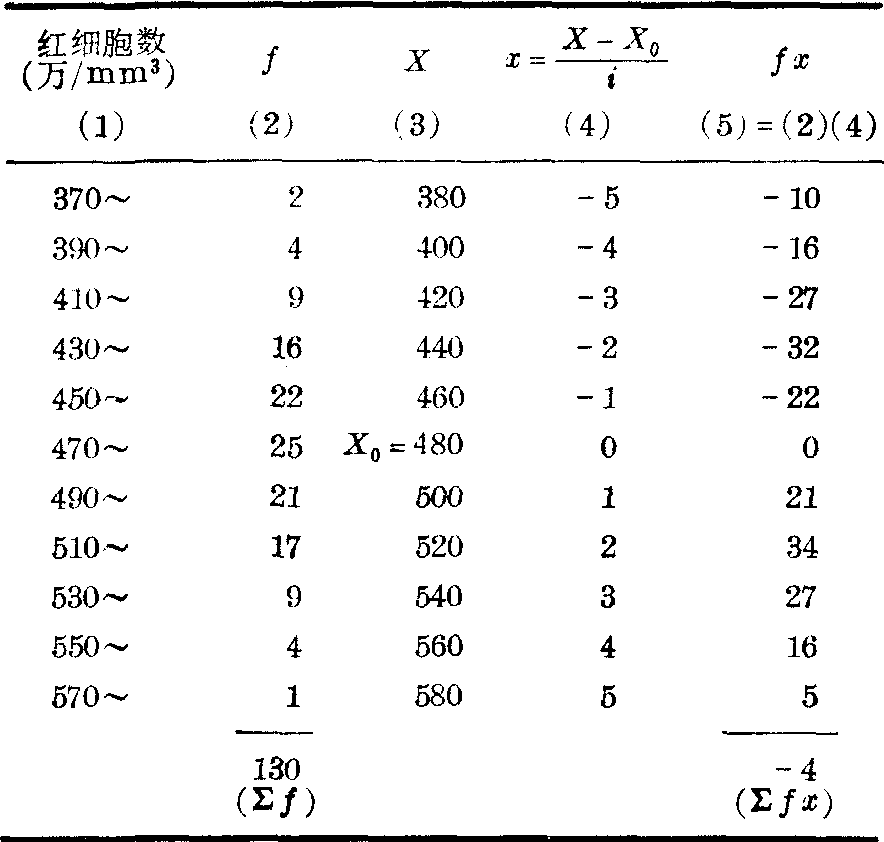
表1中i=20,∑f =130,取X0=480,∑fx=-4,按式(3)得红细胞数的均数为
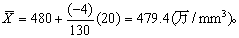
几何均数 符号为Go当一组观察值呈倍数关系,或近似倍数关系时,习惯上用倍数平均,以表示其平均水平,称几何均数。公式为
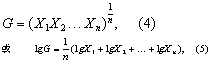
式中符号涵义同式(1)。设有4份血清的抗体效价为1:10,1:20,1:40,1:320,则
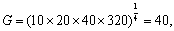
平均效价为1:40。
此类资料往往出现相同的观察值,如有f个X时,将f个X连乘,即Xf,则式(4)和式(5)可写成式 (6)和式(7):
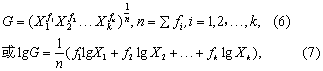
式中f1为X1的频数,余仿此,直至fk和Xk。
计算几何均数时应注意:
❶观察值中不能有0,因为0不能与任何其他数值呈倍数关系;
❷不能同时有正值和负值;
❸若全是负值,计算时可先把负号除去,得出结果后再加上负号;
❹几何均数也可以用对数计算,即按式(5)或式(7)计算后,查反对数即得G。
例4 某地对69名麻疹易感儿童接种长春47株麻疹减毒活疫苗,接种后1个月测得其血清血凝抑制效价如下,求平均效价。
| 血清稀释度倒数X | 4 8 16 32 64 128 256 512 | 合计 |
| 例数f 按式(7): | 3 4 7 11 9 15 13 7 | 69 |
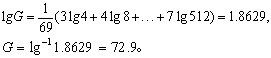
故平均效价为1:72.9。
中位数 符号为M。一组按大小顺序排列的观察值,位次居中的数值即中位数,见条目“百分位数”。用中位数表示平均水平,不受个别特小或特大观察值的影响,因此适用于:
❶资料的分布呈明显偏态;
❷分布的一端或两端无确定数值;
❸资料的分布不清。中位数的算法有直接法和频数表法。
(1)直接法: 当例数n不多时,可将观察值按大小顺序排列直接求得Mo M的位次由下式计算:
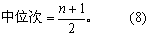
由此可见,当n为奇数时,中位数为序列位次居中的那个观察值;当n为偶数时,中位数为序列位次居中的两观察值的平均。
(2)频数表法: 当例数较多时,先将观察值编制频数表,再按式(9)或式(10)计算式(9)中n为总例数,fM为n/2所在组段的频数,i为该组段的组距,L为其下限,∑fL为小于L各组段的累计频数。式(10)中U为n/2所在组段的上限,∑fU为大于U各组段的累计频数,其他同前。当按组段由小到大累计频数时宜用式(9),由大到小累计时宜用式(10),二式所得结果相同。。
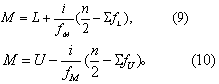
例5 某病9人的潜伏期(天)如下,求其中位数。
2 3 3 3 4 5 6 9 16
用直接法。将观察值从小到大排列,由式(8)算得:
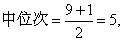
第5个观察值“4天”即该病潜伏期中位数。
例6 设例5增1例,其潜伏期为30天,求中位数。
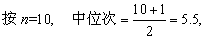
表示中位数在第5个观察
值4和第6个观察值5之间,取其均数,即得
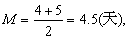
故潜伏期中位数为4.5天。
例7 145名食物中毒病人的潜伏期列于表2第(1)、(2)栏,求其中位数。
表2 粪链球菌食物中毒者的潜伏期

用频数表法。
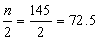
第(3)栏上部是由小到大的累计频数,下部是由大到小的累计频数,可见n/2在“12~”组段内,于是得∑fL=63,∑fv=44,L=12,U=18,i=6,fM=38。
按式(9):
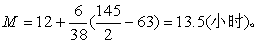
或按式(10):
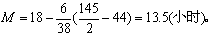
潜伏期中位数为13.5小时。
众数 符号为M0。是一组资料中出现频数最多的那个观察值。在频数表上,频数最多的那个组段的组中值可作为众数的概约估计值。按上法求得的众数称观察众数。众数还可按式(11)~(14)中任一式计算:
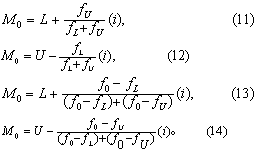
式中L为M0所在组段(即频数最多的组段)的下限: U为上限,i为组距;f0为M0所在组段的频数,fL为小于L的相邻组段的频数,fU为大于U的相邻组段的频数。同一频数表资料用式(11)和式(12) 计算结果相同,用式(13)和式(14)计算的结果相同。
同一资料分组不同时,众数也可能不同。精确的众数尚可通过频数分布曲线的拟合求得。
例8 求表1资料的众数。
表1中最大频数是25,此组段的组中值480万/mm3即观察众数。尚可按式(11)~(14)计算:
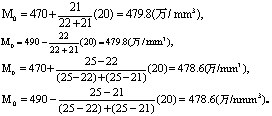
所得众数接近于观察众数480万/mm3。
均数、中位数与众数的关系: 在正态分布或其他对称分布中,X、M与M0密合; 在接近正态或对称的分布中,此三者十分接近;在轻度偏态分布中,它们有如下关系。
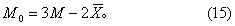
由式(15)可通过和M求M0。从式(15)还可导出式(16):
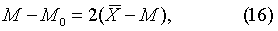
表示M在与M0之间,而且M与M0相距为M与相距之2倍。
调和均数 符号为H。调和均数是观察值X倒数之均数的倒数。常用于完成的工作量相等而完成时间不同,求平均速度。在某些假设检验中用于样本含量不同时求平均样本含量。计算公式为
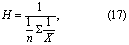
式中符号意义同前。
平均数
也称平均指标,是衡量随机变量分布的集中趋势,代表变量分布中心位置的数,是表明同一总体内各单位标志值的一般水平的指标。它把总体中各单位标志值的差异拉平、抽象化,从而得出代表总体特征一般水平的数值。如农作物的平均亩产量、营业员的平均销售额、职工的平均工资额、商品的平均价格等。其作用有: (1) 比较同时期同质的不同总体的某一数量特征,以说明不同单位、不同地区的生产水平高低或工作成绩的差别。(2)研究不同时期同一总体的某一数量特征,以说明现象的发展趋势和变化规律。(3) 分析现象间的依存关系。(4) 作为制定定额、进行预测和计算其他指标的依据。由于平均指标将总体各单位中某种数值之间的差异 (如先进与后进之间的差别等) 抽象掉,故运用时还须用分组平均数或分配数列来补充说明总平均数。平均数将总体各单位的差异作了抽象,故在社会现象中平均数只适用于根本性质相同的总体一般水平的比较。若被平均的各单位是异质的,这时利用平均数就会抹煞现象之间的本质差别,而成为“虚构的”平均数。按计算方法和所依资料不同,它可分为:算术平均数、调和平均数、几何平均数和中位数。
平均数mean
指算术平均数的简称。是同质的观测值的总和除以观测次数所得的商数,是最常用的一种集中量数,以X或M表示。常用的计算平均数的方法有两种: (1)原始数据计算法。计算公式为:X=ΣXi/n,式中Xi为各观测值数据,∑为连加符号,n为观测总量或数据总量。(2)分组计算法,又称频数分布表计算法。是原始数据计算法的导出方法。计算公式为:X=∑fiXi/n,式中fi为Xi出现的次数。计算过程是先将原始数据分组,编制出频数分布表,然后用频数分布表计算平均数。平均数充分利用了数据提供的信息,有利于进一步的统计运算,但易受极端数据的影响。
- 仲巴县是什么意思
- 仲烷基磺酸盐是什么意思
- 仲烷醇聚氧乙烯醚是什么意思
- 仲裁是什么意思
- 仲裁是什么意思
- 仲裁与诉讼的异同点是什么意思
- 仲裁协议是什么意思
- 仲裁协议分几类?是什么意思
- 仲裁协议的主要内容是什么意思
- 仲裁协议的法律效力是什么意思
- 仲裁员一般必须具备哪些条件是什么意思
- 仲裁员如何指定是什么意思
- 仲裁员超越权限是什么意思
- 仲裁审理是什么意思
- 仲裁条款、仲裁协议书是什么意思
- 仲裁检验是什么意思
- 仲裁比诉讼有啥好处?是什么意思
- 仲裁申请的一般内容是什么意思
- 仲裁的保全措施是什么意思
- 仲裁的特点是什么意思
- 仲裁的申请是什么意思
- 仲裁程序法是什么意思
- 仲裁裁决可能被法院撤销吗?是什么意思
- 仲裁裁决的一般内容是什么意思
- 仲裁裁决的形式和效力是什么意思
- 仲裁鉴定是什么意思
- 仲辛醇是什么意思
- 仲醇醚琥珀酸酯磺酸钠是什么意思
- 件件有结果是什么意思
- 价值是什么意思
- 价值分析是什么意思
- 价值分析在X型点火线圈中的应用是什么意思
- 价值分析在椭圆齿轮流量计改型中的应用是什么意思
- 价值分析在降低驳船造价中的应用是什么意思
- 价值分析对象的选择是什么意思
- 价值分析方法是什么意思
- 价值分析方法的概念是什么意思
- 价值分析的基本程序是什么意思
- 价值分析的工作程序是什么意思
- 价值分析需要的情报是什么意思
- 价值工程是什么意思
- 价值工程是什么意思
- 价值工程在19钻统一机芯三防全钢手表中的应用是什么意思
- 价值工程在PS型外文打字机色带架中的应用是什么意思
- 价值工程在T4800型收音机调谐系统中的应用是什么意思
- 价值工程在产品更新改造中的应用是什么意思
- 价值工程在原材料管理中的应用是什么意思
- 价值工程在开发X型衬玻璃隔膜阀中的应用是什么意思
- 价值工程在新产品X双端面磨床设计中的实施是什么意思
- 价值工程在洗衣机改造中的应用是什么意思
- 价值工程在自行车制管公差上的应用是什么意思
- 价值工程的一般工作程序是什么意思
- 价值工程的基本概念是什么意思
- 价值工程的定义是什么意思
- 价值消费量是什么意思
- 价值消费量是什么意思
- 价值消费量是什么意思
- 价值的概念是什么意思
- 价格是什么意思
- 价格循环论是什么意思