1.对称性:a>b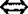 b
b
2.传递性: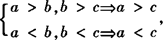 ,这两条性质是不等式证明的缩放思想的依据.
,这两条性质是不等式证明的缩放思想的依据.
3.加法法则:a>b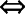 a+c>b+c(c为整式),
a+c>b+c(c为整式),
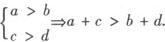
4.乘法法则:a>b,c>0 5.倒数法则: 6.乘方法则:a>b>0 7.开方法则: 例1 若a A.不等式 B.不等式 C.不等式 D.不等式 解 ∵b<0,∴—b>0,∴a—b>a, 又∵a—b<0,a<0, ∴ ∵a ∴ 由此可选B. 另外,A中 C与D中 例2 已知三个不等式: 解 对命题❷ 作等价变形: 于是,由ab>0,bc>ad可得❷ 成立,即❶ ❸ 若ab>0, 若bc>ad, ∴可组成3个正确命题. 例3 设f(x)=ax2+bx,且1≤f(—1)≤2,2≤f(1)≤4,求f(—2)的取值范围. 分析 本题考生容易错解如下: 错误的原因是三次用到了同向不等式相加的性质,导致f(—2)的取值范围的扩大. 解 设f(—2)=mf(—1)+nf(1)(m,n为待定系数), 则4a—2b=m(a—b)+n(a+b),即 4a—2b=(m+n)a—(m—n)b, ∴f(—2)=3f(—1)+f(1). ∵1≤f(—1)≤2, ∴2≤f(1)≤4, ∴5≤3f(—1)+f(1)≤10,故5≤f(—2)≤10. 以上解题过程简化如下: ac>bc,a>b,c<0
ac>bc,a>b,c<0 ac
ac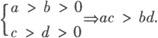
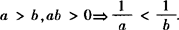 .
.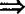 an>bn(n∈N且n>1).
an>bn(n∈N且n>1).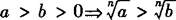 (n∈N且n>1).
(n∈N且n>1).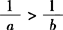 和
和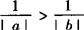 均不能成立
均不能成立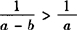 和
和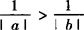 均不能成立
均不能成立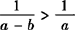 和
和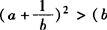
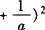 均不能成立
均不能成立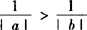 和
和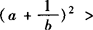
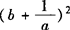 均不能成立
均不能成立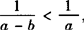 ,故
,故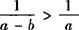 不成立.
不成立.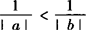 ,故
,故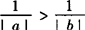 不成立.
不成立.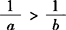 成立.
成立.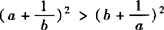 成立,其证明如下:
成立,其证明如下: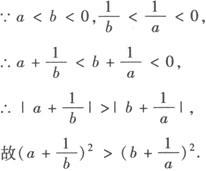
❶ ab>0,
❷ 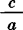
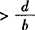 ,
,
❸ bc>ad,以其中两个作条件,余下一个作结论,则可组成( )个正确命题.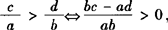 ,
,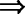 ❷ ;
❷ ;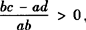 ,则bc>ad,故❶ ❷
,则bc>ad,故❶ ❷ 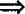 ❸ ;
❸ ;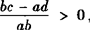 ,则ab>0,∴❷ ❸
,则ab>0,∴❷ ❸ 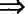 ❶ ;
❶ ;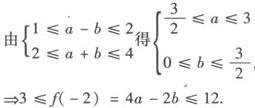
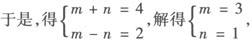
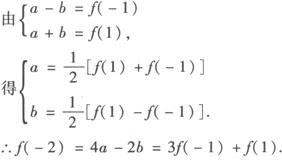
- 超声波接收器是什么意思
- 超声波控探头是什么意思
- 超声波机械加工是什么意思
- 超声波检查是什么意思
- 超声波检测器是什么意思
- 超声波油品界面检测仪是什么意思
- 超声波治疗机是什么意思
- 超声波洁牙机是什么意思
- 超声波洗涤是什么意思
- 超声波测膘仪是什么意思
- 超声波消毒是什么意思
- 超声波清冼是什么意思
- 超声波灭菌法是什么意思
- 超声波疗法是什么意思
- 超声波眼部损伤是什么意思
- 超声波裂解器是什么意思
- 超声波诊断是什么意思
- 超声波诊断仪是什么意思
- 超声波钻床是什么意思
- 超声清洗器是什么意思
- 超声焊接是什么意思
- 超声物理学是什么意思
- 超声生物物理学是什么意思
- 超声电子仪器厂是什么意思
- 超声电子计算机化x线断层扫描是什么意思
- 超声疗法是什么意思
- 超声的物理基础是什么意思
- 超声的生物效应是什么意思
- 超声示波法(a型)是什么意思
- 超声示波诊断是什么意思
- 超声脉冲回波(声)技术是什么意思
- 超声药物透入疗法是什么意思
- 超声计算机断层显像术是什么意思
- 超声诊断是什么意思
- 超声诊断仪是什么意思
- 超声诊断在计划生育中的应用是什么意思
- 超声诊断学是什么意思
- 超声诊断手册是什么意思
- 超声诊断疑难病例分析是什么意思
- 超声诊断的物理、生理和病理基础是什么意思
- 超声诊断的种类和特点是什么意思
- 超声读片指南是什么意思
- 超声透镜是什么意思
- 超声速是什么意思
- 超声速客机是什么意思
- 超声速飞机是什么意思
- 超声避孕是什么意思
- 超声钻孔是什么意思
- 超声间动电复合疗法是什么意思
- 超声雾化是什么意思
- 超声雾化吸入是什么意思
- 超声雾化吸入法是什么意思
- 超声雾化吸入疗法是什么意思
- 超声雾化器是什么意思
- 超声频移诊断是什么意思
- 超声频移诊断法是什么意思
- 超声频(率)是什么意思
- 超声风速表是什么意思
- 超声鱼群探测器是什么意思
- 超复杂细胞是什么意思