仿紧空间的广泛应用,引起了对仿紧性的形形色色的推广,形成覆盖性质理论。
绝大部分的覆盖性质都能使“可数紧闭子集成为紧子集”(这一性质称为iso-紧性)。不可约(irreducible)空间引起人们的兴趣是从1950年阿伦等(Arens-Dugundji)利用弱仿紧(metacompact)空间的不可约性证明了“弱仿紧的可数紧空间是紧空间”开始的。
以后人们一方面寻找哪些类型的空间具有不可约性,另一方面发现了不可约性的类似于使可数紧性成为紧性的一些作用。
这样,就使不可约性在拓扑空间理论中,特别是覆盖性质方面起著很大作用。
空间X的开覆盖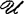 称为最小的,如果不存在
称为最小的,如果不存在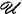 的真子族覆盖X,空间X称为不可约的,如果X的每一开覆盖具有最小的加细开覆盖。空间X称为θ-加细的(θ-refinable),如果X的每一开覆盖
的真子族覆盖X,空间X称为不可约的,如果X的每一开覆盖具有最小的加细开覆盖。空间X称为θ-加细的(θ-refinable),如果X的每一开覆盖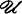 存在加细开覆盖序列{
存在加细开覆盖序列{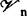 }n∈N,对每一x∈X,存在n(x)∈N使0<ord(x,
}n∈N,对每一x∈X,存在n(x)∈N使0<ord(x,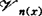 )<ω;称为弱θ-加细的(weaklyθ-refinable),如果X的每一开覆盖
)<ω;称为弱θ-加细的(weaklyθ-refinable),如果X的每一开覆盖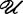 存在加细开覆盖
存在加细开覆盖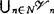 ,对每一
,对每一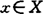 ,存在n(x)∈N,使
,存在n(x)∈N,使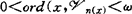 ;如果在弱θ-加细空间的定义中更添加:{
;如果在弱θ-加细空间的定义中更添加:{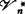 }是点有限的(
}是点有限的(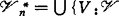 ∈Vn}),则称X为弱
∈Vn}),则称X为弱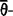 加细的(weakly
加细的(weakly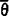 -refinable)。
-refinable)。
熟知弱仿紧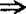 θ-加细
θ-加细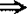 弱
弱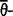 加细
加细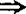 弱θ-加细,而相反蕴含关系都不能成立。
弱θ-加细,而相反蕴含关系都不能成立。
1975年蓬奈(Boone)证明:“θ-加细空间是不可约的”,并提出问题:“弱θ-加细空间是否不可约?”1977年度文(VanDouwen)等否定地回答了这问题,他们构作了一个正则、弱θ-加细而非不可约的空间。
1975年斯密司(Smith)引入了弱θ-加细空间。弱θ-加细空间是否不可约引起人们的兴趣。
1976年蓬奈证明:“弱θ-加细空间是不可约的”。
斯密司曾提出问题:“可数弱仿紧的弱θ-加细空间是否弱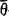 -加细空间?”随著上述结果的证明,把上述问题改写为问题1:“可数弱仿紧的弱θ-加细空间是否不可约?”这问题尚未解决。
-加细空间?”随著上述结果的证明,把上述问题改写为问题1:“可数弱仿紧的弱θ-加细空间是否不可约?”这问题尚未解决。
蓬奈曾给出不可约空间的一个有效的刻划:“空间X是不可约的,当且仅当X的每一开覆盖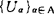 存在离散闭集族
存在离散闭集族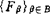 使
使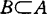 ,
,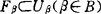 且
且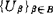 覆盖X”。
覆盖X”。
易知可数紧空间的每一离散集族是有限的,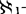 紧空间(每一不可数子集有聚点)的每一离散集族是可数的(也称为性质(δ),易知性质(δ)等价于
紧空间(每一不可数子集有聚点)的每一离散集族是可数的(也称为性质(δ),易知性质(δ)等价于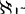 紧,而Lindelof空间具有性质(δ))。由上述刻划得下述定理:“在不可约空间:
紧,而Lindelof空间具有性质(δ))。由上述刻划得下述定理:“在不可约空间:
❶ 可数紧性与紧性等价。
❷ 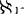 紧性与Lindelof性质等价。
紧性与Lindelof性质等价。
”这定理显示了不可约空间的有趣的性质。
从本文开端的叙述似乎不可约性与iso-紧性有蕴含关系,其实不然。弱θ-加细空间是iso-紧的,但不是不可约的,此外,有反例说明:不可约性+集态正规性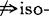 紧性,这由于不可约性不是闭遗传的。
紧性,这由于不可约性不是闭遗传的。
空间X称为δθ-加细的、弱δθ-加细的、弱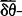 加细的,如果把θ-加细的、弱θ-加细的、弱
加细的,如果把θ-加细的、弱θ-加细的、弱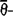 加细的定义中的“
加细的定义中的“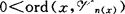 <∞”分别改为
<∞”分别改为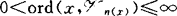 ”。
”。
斯密司在引入弱θ-加细空间后曾证明θ-加细性蕴含弱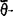 加细性,但在引入弱
加细性,但在引入弱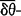 加细空间后他不知是否有类似的蕴含关系。故有问题2:“δθ-加细空间是否弱
加细空间后他不知是否有类似的蕴含关系。故有问题2:“δθ-加细空间是否弱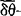 加细的?”这问题尚未解决。
加细的?”这问题尚未解决。
1984年马虚磐(Mashburn)证明:“T1的δθ-加细空间,T1的弱δθ加细空间都是不可约的”。必须指出条件T1不能去掉。
但他是对δθ-加细空间、弱δθ-加细空间分别证明的,并没有解决问题2。
1972年磐奈(Bennett)等把完全性附加于弱θ-加细空间,得到:“完全的,弱θ-加细空间是次仿紧的,从而是不可约的。”
1977年刘应明引入拟仿紧性与狭义拟仿紧性,按狭义拟仿紧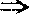 拟仿紧,且θ-加细
拟仿紧,且θ-加细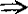 狭义拟仿紧,故有:拟仿紧空间是否不可约的?”这问题已为朱俊(1991)正面地解决:“T1拟仿紧空间是不可约的”。但条件T1不能去掉。
狭义拟仿紧,故有:拟仿紧空间是否不可约的?”这问题已为朱俊(1991)正面地解决:“T1拟仿紧空间是不可约的”。但条件T1不能去掉。
不可约空间的遗传性及映射性质。很多的覆盖性质具有闭遗传性,特别是具有Fσ-遗传性(即每-Fσ子空间保持原来空间的性质)。
例如:仿紧、弱仿紧、次仿紧、θ-加细、弱θ-加细、δθ-加细、弱δθ-加细等等,因此,再附加条件“完全性”后可获得遗传性。对不可约空间来说,情况未必尽然。
不可约空间不具有闭遗传性。1976年度文宣称“每一空间可以作为闭子集浸没于某一不可约空间”,未见其构造。
1979年代维斯(Davis)等给出了构造。对任一空间X可以构造不可约空间g(X)使X同胚于g(X)的某闭集且变换g保持势(无限情况)、特征(character)、分离性及集态正规性等。
不可约空间虽不具有闭遗传性,可有下述有趣结果(困完全的次仿紧空间是遗传性次仿紧的):“完全的、弱θ-加细空间是遗传性不可约空间”。这定理之所以有趣是弱θ-加细空间未必具有不可约性。至于是否可用“不可约”代替上述定理中的“弱θ-加细”,我们提出如下问题3:“完全的、不可约空间是否遗传性不可约的?”
上述问题已为朱俊(1991)否定地解决,他证明:“完全的、不可约空间是开遗传的,未必是闭遗传的。”
关于不可约空间的映射性质的讨论。
我们提出问题4:“不可约空间能否为闭(完备)映射所保持?”这问题尚未解决,朱俊(1991)曾给出这问题部分解答:
❶ T1拟仿紧空间的闭象是不可约的。
❷ 设X不可约,A闭于X,则X/A是不可约的。
❶ 中的条件T1不能去掉。
【参考文献】:
1 Bennett H R, et al. Gen Top Appl, 1972,2:49~54
2 Smith J C. Proc Amer Math Soc, 1975,53:511~517
3 Boone J R. Bull Austral Math Soc, 1975,12:143~148
4 Smith J C. Proc Amer Math Soc, 1976,57; 133 ~139
5 Boone J R. Pacific J Math, 1976,82:351 ~ 357
6 Van Douwen E, et al. Houston J Math, 1977,3:141~152
7 刘应明.数学学报,1977,20∶212~214
8 Mashburn J D.Top.Proc,1984,9∶339~352
9 高国士.数学进展,1989,18∶143~149
10 朱俊.数学学报,1991,34∶309~315
(苏州大学高国士教授撰)
下一篇:现代科技综述大辞典上目录
是指投保人违反如实告知义务致使保险人有权解除保险合同或者不负给付保险金责任的,经过保险合同特约的期间后,保险人不得以投保人违反如实告知义务而拒绝保险合同约束力的条款。不可争议条款作用的对象,为可争议期间内的可争议事项;若经过可争议期间,保险人没有对可争议事项进行争议,则不得再对之进行争议。不可争议条款的典型条款,为年龄误保条款。投保人申报的被保险人年龄不真实,并且其真实年龄不符合保险合同约定之年龄限制的,保险人可以解除合同,并在扣除手续费后,向投保人退还保险费;但是,自保险合同成立之日起经过2年的,不在此限。被保险人或者受益人援引不可争议条款时,不论投保人在订立保险合同时是否如实告知所有重要情况,只要保险合同成立后经过法定或者约定的不可争议期间,保险人不得再以违反如实告知义务主张解除合同或者拒绝承担保险责任。
- 稻田养鱼技术推广是什么意思
- 稻田养鸭技术是什么意思
- 稻田守是什么意思
- 稻田守丛草吏是什么意思
- 稻田护肤膏是什么意思
- 稻田提举司是什么意思
- 稻田深处草虫鸣.是什么意思
- 稻田灌溉是什么意思
- 稻田生态渔业是什么意思
- 稻田生态种养新技术是什么意思
- 稻田耕一郎是什么意思
- 稻田苇莺是什么意思
- 稻田蜘蛛利用研究是什么意思
- 稻田衣是什么意思
- 稻田衲是什么意思
- 稻田里干活——拖泥带水是什么意思
- 稻田里拉犁耙是什么意思
- 稻田里插秧——以退为进是什么意思
- 稻田里的害草是什么意思
- 稻畦是什么意思
- 稻畦帔是什么意思
- 稻畦明月家家酒,茅屋清歌处处霜。是什么意思
- 稻瘟净是什么意思
- 稻瘟灵是什么意思
- 稻瘟病是什么意思
- 稻瘟病菌生理小种的研究是什么意思
- 稻瘟酞是什么意思
- 稻瘟霉素是什么意思
- 稻瘤矮病是什么意思
- 稻瘿蚊是什么意思
- 稻白叶枯病是什么意思
- 稻的一种是什么意思
- 稻的初生幼苗是什么意思
- 稻的外壳是什么意思
- 稻的起源是什么意思
- 稻真前翼甲螨是什么意思
- 稻眼蝶是什么意思
- 稻矮缩病是什么意思
- 稻秀雨浇,麦秀风摇是什么意思
- 稻秆是什么意思
- 稻秆墩是什么意思
- 稻秆株𩪘是什么意思
- 稻秆绳是什么意思
- 稻秆蝇是什么意思
- 稻秆衣是什么意思
- 稻秆袽是什么意思
- 稻种是什么意思
- 稻种宝是什么意思
- 稻秧是什么意思
- 稻秫是什么意思
- 稻秫圪兰是什么意思
- 稻秫圪榄是什么意思
- 稻秫面是什么意思
- 稻秸是什么意思
- 稻秸子是什么意思
- 稻稿是什么意思
- 稻稿草是什么意思
- 稻穗是什么意思
- 稻穗瘤蛾是什么意思
- 稻穗越长得丰满,身子弯得越低是什么意思