射影面积定理sheying mianji dingli

一个平面图形上所有的点在一个平面上的射影的集合叫做这个平面图形在该平面上的射影.若原平面图形的面积为S，它所在的平面与射影平面所成的二面角为α，射影图形的面积为S′，则S′=S·cosα.
例 棱柱的底面是边长为α的正六边形，侧面都是正方形（如图），过它的下底面的一边和同它所对上底面的一边作截面，求截面面积.

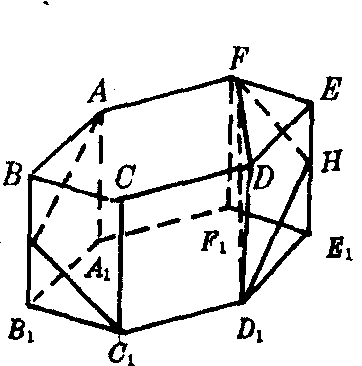
解 不难作出过AF和C₁D₁的截面AGC₁D₁HF，连结D₁F,DF.容易证明∠D₁FD是截面与下底面所成二面角的平面角.正六边形ABCDEF为截面在下底面内的射影图

形. 因为

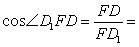
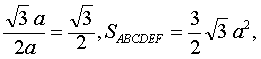
所以

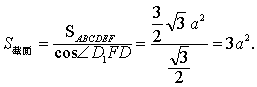
有时还可利用上述定理求二面角的大小.事实上，在公式S′=Scosα中含有三个量S′,S,a，若已知其中的任意两个，便可求出另一未知量.