a.化简要求:
❶ 能求出值的应求出值.
❷ 使用三角函数种数尽量少.
❸ 使项数尽量少.
❹ 尽量使分母不含三角函数.
❺ 尽量使被开方数不含三角函数.
b.三角恒等式的证明,就是合理准确灵活地选用基本三角恒等式进行三角函数的等价变换,原则由繁到简.
例1 函数y=2sinx(sinx+cosx)的最大值为( ).

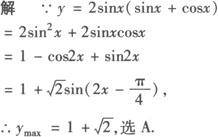
例2 证明
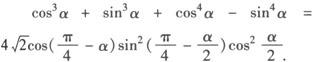
证明 等式两边都较复杂,可采用左右归一的途径.
左边=(cosα+sinα)(cos2α—cosαsinα+sin2α)+(cos2α+sin2α)·(cosα+sinα)(cosα—sinα)=(cosα+sinα)(1—cosαsinα+cosα—sinα)=(cosα+sinα)(1+cosα)(1—sinα),
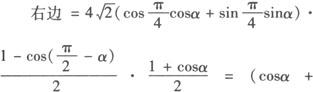
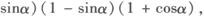
∴左边=右边,原式成立.
例3 设θ和φ均为锐角,且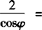
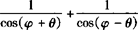 ,求证:
,求证: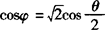
分析 观察比较条件与结论,知切入点应在条件右端,通过变换使φ与θ分离,同时实现角的结构转变:“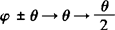 ”.
”.
证明
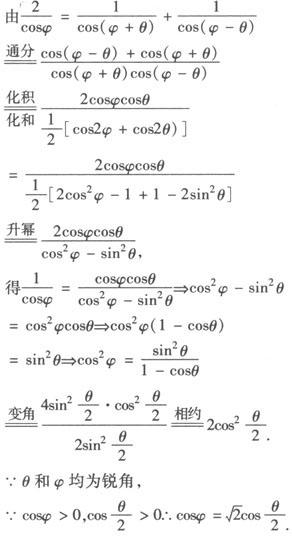
- 出车是什么意思
- 出车合辙是什么意思
- 出车时间利用系数是什么意思
- 出车殄寇是什么意思
- 出车院是什么意思
- 出轨是什么意思
- 出轨受耻辱是什么意思
- 出轨(鬼)了是什么意思
- 出转勃转是什么意思
- 出轻入量是什么意思
- 出辔头是什么意思
- 出辞气,斯远鄙倍矣。是什么意思
- 出辭氣是什么意思
- 出辱下殿是什么意思
- 出迎是什么意思
- 出运是什么意思
- 出运前出口信用保险是什么意思
- 出运前风险保险是什么意思
- 出运后出口信用保险是什么意思
- 出运险是什么意思
- 出迓是什么意思
- 出还 - 韦应物 - 昔出喜还家,今还独伤意。入室掩无光,衔哀写虚位。凄怆动幽幔,寂寂惊寒吹。 幼女复何知?时来庭下戏。咨嗟日复老,错莫身如寄。家人劝我是什么意思
- 出进是什么意思
- 出进口厂商辅导管理办法是什么意思
- 出远门是什么意思
- 出远门儿是什么意思
- 出连是什么意思
- 出连乞都是什么意思
- 出连虔是什么意思
- 出连部是什么意思
- 出连高胡是什么意思
- 出迟是什么意思
- 出退是什么意思
- 出送是什么意思
- 出送日是什么意思
- 出适是什么意思
- 出逃是什么意思
- 出造是什么意思
- 出連是什么意思
- 出進是什么意思
- 出道是什么意思
- 出郊是什么意思
- 出郊劝农八绝(选五首)是什么意思
- 出郊开帐饮,寅饯盛离章。是什么意思
- 出郊观猎至贺兰山是什么意思
- 出郊观猎至贺兰山 (明)金幼孜是什么意思
- 出部是什么意思
- 出郭晓色微,临水人意静。水上寒雾生,弥漫与天永。折苇动有声,遥山淡无影。稍见初日升,三两列舴艋。安得学野凫,泛泛逐清影。是什么意思
- 出郭都无三十里,同行恰有两三人。是什么意思
- 出都留别诸公是什么意思
- 出都留别诸公(选一) - 康有为是什么意思
- 出都门留别诸公是什么意思
- 出配是什么意思
- 出酒令行酒是什么意思
- 出醋儿是什么意思
- 出醜是什么意思
- 出醺讲是什么意思
- 出里出拉是什么意思
- 出重是什么意思
- 出针是什么意思