信号的频域分析

把信号看成由不同频率的正弦波组合而成，并以频率为自变量进行分析，称为信号的频域分析，这是一种描述信号的有效方法。以频率为横座标描述信号包含的不同频率成分的幅度或相位关系的图形称为频谱，频谱概念是分析处理信号的重要工具。
富氏 (Fourier)级数与离散频谱 大多数连续周期信号都可以分解为一组正弦波的组合，表达这些正弦波间幅度和相位关系的数学公式称为富氏级数，反映连续周期信号频率特性的频谱为非周期的离散频谱。
(1)富氏级数： 连续周期信号的富氏级数复数表达式为

其中，Ck和φK分别为k次谐波的幅度和相位。例如，图1(a)所示的周期脉冲波可以分解成图1(b)所示一系列正弦波（图上只画出四种）。其中恒定不变的称为直流分量，频率和原波形相等的正弦波称为基波，频率比基波高k倍的正弦波称为k次谐波。分解出的各正弦波的特征除了可由它们的频率和振幅表示外，还和它们的初相位有关。初相位表示各正弦波之间的相对关系，它对合成波形的形状有显著影响。例如图2(a)、(b)是由两组频率和振幅相同的基波和二次谐波合成的。但由于两图中各分量的相对相位不同，合成的波形相差便很大。

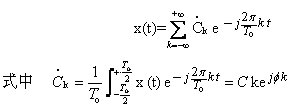
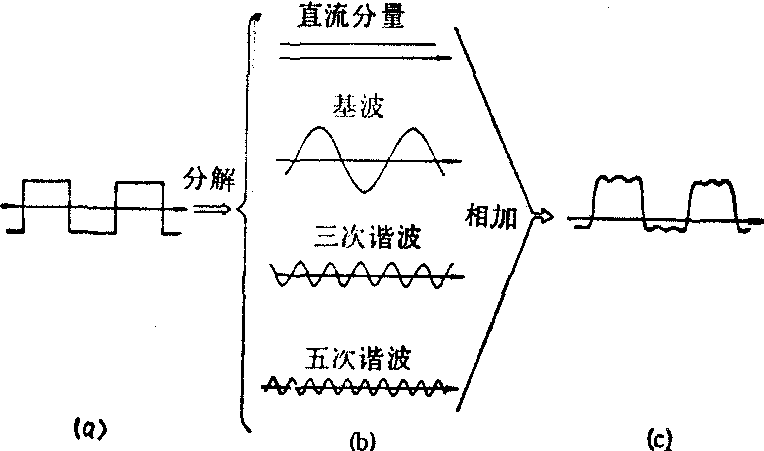
图1 周期性脉冲波形的分解

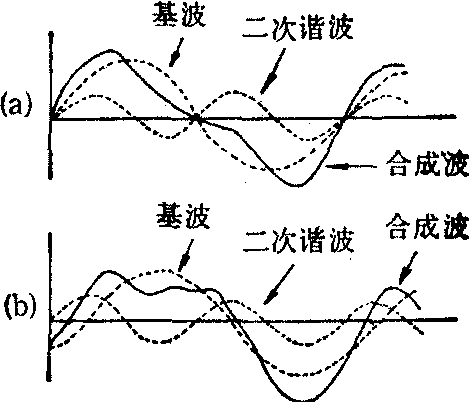
图2 初相位对合成波形的影响

(2) 离散频谱： 连续周期信号的离散频谱以频率f为横座标，分别以其按富氏级数分解的正弦波及直流分量的幅度C_k和初相位φ_K为纵座标，如图3(a)所示。图左表示各频率成分的振幅，称为振幅频率特性，简称幅频特性。图右表示各频率成分的初相位，称为相位频率特性，简称相频特性。由于周期函数只在基本频率f₀＝1/T₀及其整数倍处有频率成分（基波和谐波），因此图象只在若干离散的频率处呈现谱线，称为离散频谱。在工程分析中常把幅度值CK减小一半，对称地画在直流分量左右两侧，如图3(b)所示。在这种表示形式中，谱线既出现在正频率轴上，也出现在负频率轴上，但负频率是为数学分析的便利而引入的，没有物理意义。

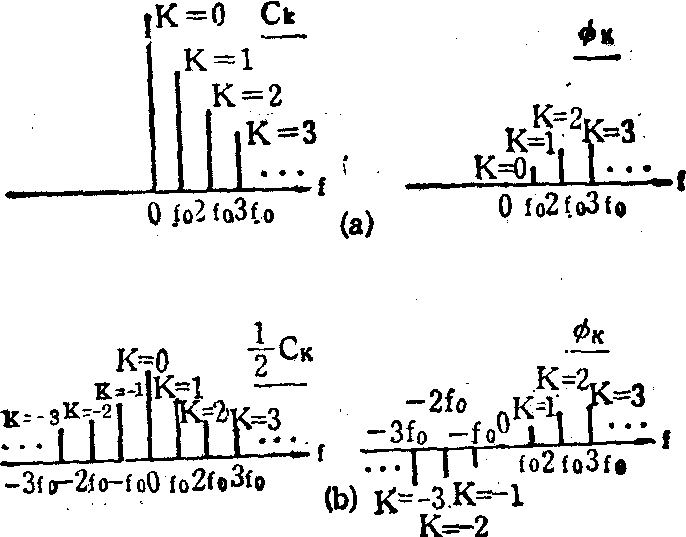
图3 连续周期信号的离散频谱

当信号的幅频和相频特性已知后，当然也能把各正弦波迭加起来恢复信号的原波形，如图2所示。
富氏(Fourier)变换和连续频谱非周期连续信号可以分解成无穷个频率连续而幅度无穷小的正弦波，这些正弦波的幅度和相位间存在的固定的数学关系，称为富氏变换。非周期的连续信号的频谱为连续频谱。和离散频谱一样，连续频谱也可分别表示为幅频特性和相频特性，如图4表示。

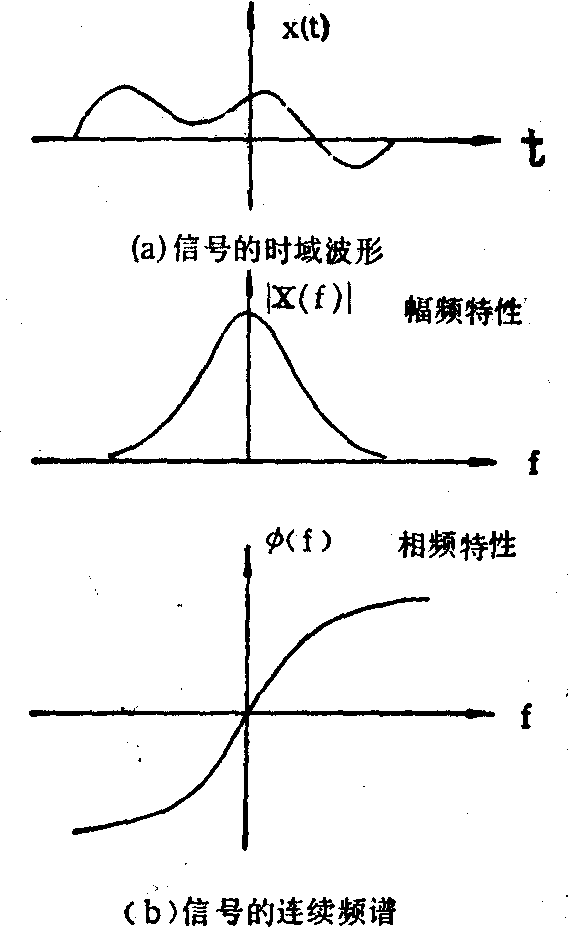
图4 非周期的连续信号的连续频谱

反过来，由信号的连续频谱也能迭加成信号的原波形，这一过程称为反演富氏变换。
设X(t)为非周期的连续信号，则其富氏变换为X(f)=

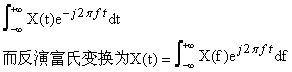
频域中的滤波器概念 各种滤波器都是从频域概念上建立起来的，不同频率的正弦波通过滤波器后，衰减程度各不相同。以频率为横座标，以输出与输入正弦波的幅度比值为纵座标，可以表示滤波器对信号中包含的不同频率成分的传输特性，如图5所示。图5(a)所示的滤波器容易通过低频成分，而衰减高频成分，称为低通滤波器；图5(b)、(c)、(d)分别为高通、带通、带阻滤波器的特性。这些滤波器广泛应用于各种生物阻医学电子仪器中。例如，止带在50Hz的带阻滤波器可去除I频干扰；电生理信号的频谱通常比较低，在这些仪器中通常要采用低通滤波器来滤除高频的干扰和噪声； 超声多普勒血

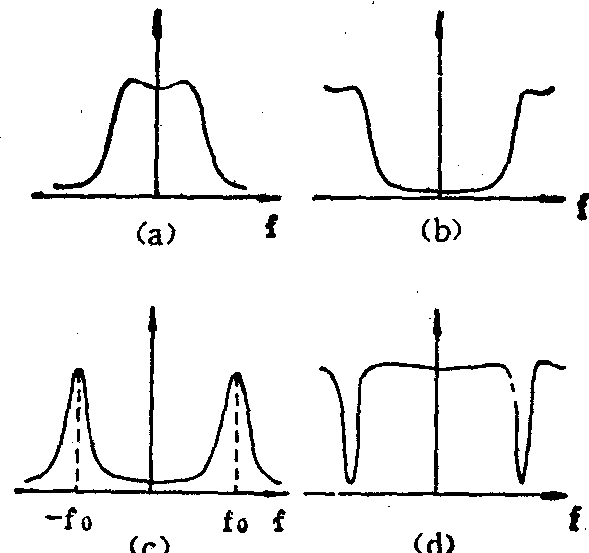
图5 几种滤波器的幅频特性
(a)低通 (b)高通 (c)带通 (d)带阻

流计中用带通滤波器消除血管壁运动引起的低频干扰和正交检测引起的高频成分。
采样后信号的频谱 设连续信号X(t)的频谱是X(f)，以采样频率fs=1/Ts对X(t)采样后的信号为X(n)，则采样后信号X(n)的频谱X′(f)是采样前信号X(t)的频谱X(f)的周期性移动和重复，如图6所示。图6中，(a)为采样前信号X(t)和频谱X(f)的图形；(b)为采样后信号X(n) 和频谱的图形。采样后频谱的重复周期=采样频率fs。如果采样频率fs足够高，移位后的谱不与原谱交迭，则可用适当的低通滤波器(其特性如图6(b)虚框所示)把原谱提取出来，从而恢复原信号。但是，如果采样率不够高，移位后的谱就会和原谱互相混迭，如图6(c)所示，不可能用滤波器来恢复原信号。采样后不发生频谱混迭的条件是采样率大于奈奎斯特(Nyqust)频率。

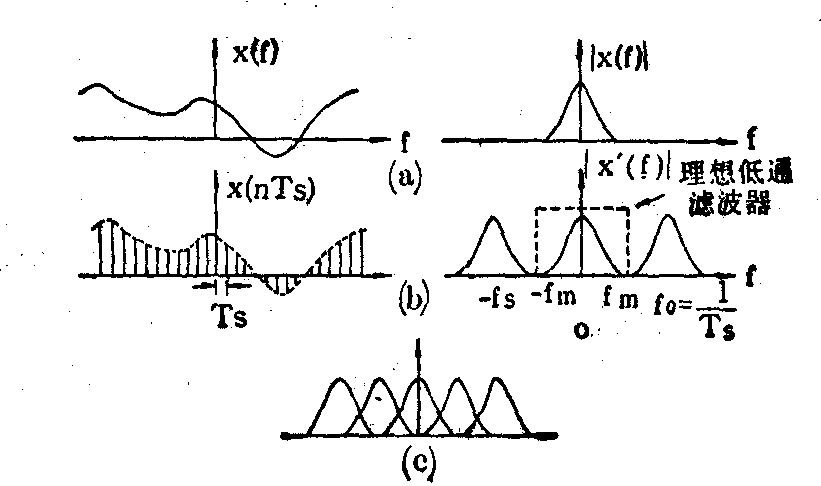
图6 采样后信号的频谱

离散富氏变换(DFT)和快速富氏变换(FFT) 将采样后的一组离散的时间序列信号变换为一组离散的频谱值的富氏变换，称为离散富氏变换。离散富氏变换的目的是适应数字计算机的特点，把富氏变换的运算离散化。为减少进行离散富氏变换的计算量的快速算法，称为快速富氏变换。离散富氏变换是从输入信号的采样序列X(n)中取N点样本(n=0～N-1)，通过一定数学计算得到f=0～fs区间内的N个离散谱值X(k△f)(k=0～N-1)，其间距为△f=fs/N。如图7所示。离散富氏变换的数学计算公式为：

反过来，由X(k)的N个采样(k=0～N-1)也能算出原序列x(n)的N个值，这种变换称为反演离散富氏变换，其数学计算公式为

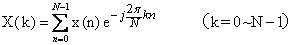
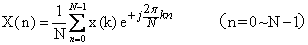
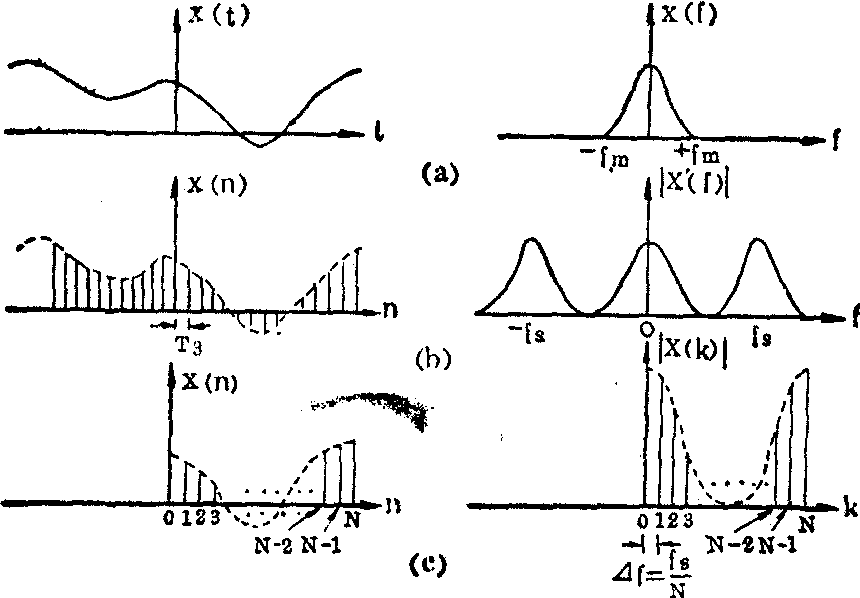
图7 离散富氏变换

应用离散富氏变换时应注意：
❶采样率需满足奈奎斯特条件fs≥2fm，否则会引起频谱混迭；
❷由于用来计算离散富氏变换的只是实际数据的N点采样值，不可能完整反映信号的全过程，因此计算结果与真实值之间存在误差；
❸频率分辨率： 变换所得只是N个离散频率处的谱值，相邻谱线的频率间隔是Δf=fs/N，称为频率分辨率，要提高分辨率只能增加数据点数N。
直接按上面两式进行离散富氏变换，其计算工作量较大，难以进行实时处理。为此研究出各种快速算法，以减少进行富氏变换时所需要的计算量 （主要是乘法次数）。自从1965年Cooleg和Tukey提出第一种快速算法以来，陆续问世的快速算法很多，其中用得最普遍的是以2为基的算法。所谓“以2为基”，其含义是：参与变换的数据总数N是2的整数幂(例如28=256,29=512,210=1024等)，当实际数据N不是2的整数幂时，可以先在数据尾部补零，从而凑成2的整数幂。离散富氏变换的快速算法统称快速富氏变换(FFT),FFT本身纯属数学计算的技巧，并无任何物理意义。在实际工作时可以采用已编就的FFT程序。只要向计算机输入数据点数N和原始数据x(0)～x(N-1)〔或X(0)～X(N-1)〕，再调用程序就可以获得DFT〔或反演DFT〕结果。
作FFT前先要确定采样率fs=1/Ts和数据点数N。fS决定于奈奎斯特条件fs≥2fm，通常多取fS=(5-10)fm。N决定于所要求的频率分辨率。例如，设心电信号的fm=100Hz，可取采样率fS=500Hz(即采样间隔TS=1/fS=2 ms)。如果希望频率分辨率Δf=0.5Hz，则N=fS/Δf=1000，可取1024点。此时被采的数据总长度是NTS=2秒，约为两个心电图周期。