仿射坐标变换
仿射坐标变换fangshe zuobiao bianhuan
设已给两个仿射坐标系σ=〔O;e1,e2,e3〕,σ′=〔O′;e′1,e′2,e′3〕,σ叫做旧坐标系,σ′叫做新坐标系,把σ′的底矢e′1,e′2,e′3写成σ的底矢e1,e2,e3的线性组合
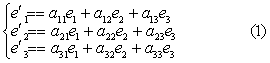

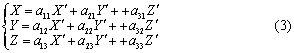
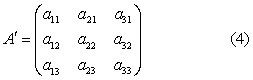
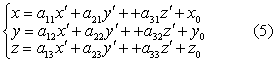
☚ 仿射坐标系 仿射坐标系下二次曲面的标准方程 ☛
- 先喻后正是什么意思
- 先喻后正的写作手法是什么意思
- 先嗇是什么意思
- 先嗣是什么意思
- 先嗰排是什么意思
- 先回是什么意思
- 先国后己是什么意思
- 先国家之急而后私仇。是什么意思
- 先国家之急而后私仇也。是什么意思
- 先国家之急,而后私也。是什么意思
- 先圣是什么意思
- 先圣先师是什么意思
- 先圣后圣,其揆一也。是什么意思
- 先圣大训是什么意思
- 先圣太师庙是什么意思
- 先圣庙是什么意思
- 先圣本纪是什么意思
- 先圣王成其身而天下成,治其身而天下治是什么意思
- 先圣遗范是什么意思
- 先圣(孔子)生卒年月日考是什么意思
- 先坎离丸是什么意思
- 先垄是什么意思
- 先域是什么意思
- 先培养你的嗅觉,再掏空你的腰包是什么意思
- 先培训后就业是什么意思
- 先培训后就业的原则是什么意思
- 先培训,后就业是什么意思
- 先墓是什么意思
- 先增长后再分配战略是什么意思
- 先增长后分配是什么意思
- 先壟是什么意思
- 先声是什么意思
- 先声后实是什么意思
- 先声夺人是什么意思
- 先声而后实者是什么意思
- 先处战地而待敌者佚,后处战地而趋战者劳。是什么意思
- 先处理事情再报告上级是什么意思
- 先处理后报告是什么意思
- 先外祖是什么意思
- 先夜子是什么意思
- 先大夫是什么意思
- 先大父是什么意思
- 先天是什么意思
- 先天下之忧而忧后天下之乐而乐是什么意思
- 先天下之忧而忧(打三国人名二)乐进、甘后是什么意思
- 先天下之忧而忧,后天下之乐而乐是什么意思
- 先天下之忧而忧,后天下之乐而乐。是什么意思
- 先天下之忧而忧,后天下之乐而乐(宋·范仲淹《范文正公集·七·岳阳楼记》)是什么意思
- 先天不足是什么意思
- 先天与后天是什么意思
- 先天之本是什么意思
- 先天之火是什么意思
- 先天之神是什么意思
- 先天之精是什么意思
- 先天之精气是什么意思
- 先天免疫性是什么意思
- 先天八卦是什么意思
- 先天八卦图是什么意思
- 先天八卦圖是什么意思
- 先天具备的认识能力是什么意思