向量间的乘积

---

两个向量a与b的数量积定义 a与b的数量积，记为a·b(或称点积)，规定如下：

记号为向量a与b之间不超过π的角．

数量积满足下列规则

交换律：a·b=b·a．

结合律：λ(a·b)=(λa)·b=a·(λb)．

分配律：a·(b+c)=a·b+a·c，

其中λ为实数．

数量积的计算公式 设a=｛x₁，y₁，z₁｝，b=｛x₂，y₂，z₂｝，则

a·b=x₁x₂+y₁y₂+z₁z₂．

两个向量a，b的垂直充要条件是a·b=0或x₁x₂+y₁y₂+z₁z₂=0．

向量a在向量b上的投影ab

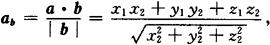
其中a=｛x₁，y₁，z₁｝，b=｛x₂，y₂，z₂｝．

两个向量的夹角公式 设a=｛x₁，y₁，z₁｝，b=｛x₂，y₂，z₂｝．则

两个向量a与b的向量积(或叉积)定义 两个向量a，b的向量积是满足下列条件的一个向量，记作a×b(又称叉积)：

(1)a×b⊥a，a×b⊥b；

(2)|a×b|=|a||b|sin(a，b)，即其模为以a，b为邻边的平行四边形的面积；

(3)a，b，a×b构成右手系，即以右手的大拇指的指向为a，食指的指向为b，则中指指向a×b．

基本单位向量i，j，k的叉积关系

i×j=k，j×k=i，k×i=j，

j×i=－k，k×．j=－i，i×k=－．j．

叉积的运算规则

a×a=0；

a×b=－b×a；

(λa)×b=a×(λb)=λ(a×b)，λ为实数；

a×(b+c)=a×b+a×c；

(a+b)×c=a×c+b×c．

叉积的计算公式 设a=｛x₁，y₁，z₁｝，b=｛x₂，y₂，z₂｝，则

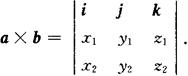
两向量平行的充要条件 a×b=0．

三个向量的混合积定义 a·(b×c)

|a·(b×c)|的几何意义 以a，b，c为邻边的平行六面体的体积．

三个向量共面的充要条件 a·(b×c)=0．

混合积的计算公式 设a=｛x₁，y₁，z₁｝，b=｛x₂，y₂，z₂｝，c=｛x₃，y₃，z₃｝，则

混合积性质 a·(b×c)=(a×b)·c=－(a×c)·b=－(b×a)·c．

三个向量的向量积

(1)a×(b×c)=(a·c)b－(a·b)c．

(2)a×(b×c)+b×(c×a)+c×(a×b)=0．