稳态性能

---

稳态误差是描述系统稳态性能的一种性能指标，通常在阶跃信号、斜坡信号或加速度信号作用下进行测定或计算。如果当时间趋于无穷大时，系统的输出量不等于输入量或输入量的确定函数，则认为系统存在稳态误差。稳态误差是系统控制精度或抗干扰能力的一种度量，

4．2．1 稳态误差的定义

系统的误差定义为希望输出与实际输出之差，即

E(s)=C₀(s)－C(s) (1．9－52)

式中 E(s)为一误差象函数；C₀(s)为一希望(理想)的输出量象函数；C(s)为一实际输出量象函数。由图1．9－38可知C₀(s)=R(s)μ(s)，式中μ(s)为理想系统传递函数．可以证明μ(s)=1／H(s)．于是，式(1．9－52)可写成

误差本身是时间t的函数，对式(1．9－53)进行拉氏反变换，可得误差原函数e(t)为

e(t)=L^－1〔E(s)〕=L^－1〔Φ_e(s)R(s)〕(1．9－54)

误差e(t)包含暂态分量与稳态分量两部分，如果系统是稳定的，过渡过程结束后，误差信号中的暂态分量必趋于零，剩下的只有稳态分量。因此，控制系统的稳态误差可定义为误差信号的稳态分量，以e_ss(t)表示，即

解：首先计算由输入信号单独作用时系统的稳态误差e_ssr(t)．对输入而言，系统为Ⅰ型单位反馈控制系统，其开环增益K=10。由表1．9－8可知，系统由输入信号引起的稳态误差为

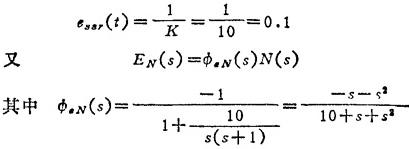
将Φ_aN(s)的分子分母进行长除，可求得

c₀=0，c₁=－0．1，c₂=－0．09，c₃=0．019…

扰动及其各阶导数为

n(t)=0．1sjnf，n(t)=0．1cost．n⁽²⁾(t)=－0．1sint，n^(s)(t)=－0．1cost…

则系统由扰动引起的稳态误差为

e_san(t)=c₀n(t)+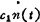+c₂n⁽²⁾(t)+_c3ⁿ⁽⁸⁾(t)+…=－0．0119cost+0．009sint=0．015sin(t－52．9°)

由于线性系统满足叠加原理，系统在输入和扰动同时作用下的稳态误差为

e_ss(t)=e_ssr(t)+e_ssn(t)=0．1+0．015sin(t－52．9°)

系统最大误差为：0．1+0．015=0．115。