概率加法公式

---

或称概率加法定理。

指事件A与B的和事件是由事件AB至少出现其中之一所组成的事件，记作A+B，对于两个互相排斥的事件A与B之和事件的概率，等于该两事件的概率之和。设已知事件A出现的概率为P(A)，事件B出现的概率为P(B)，则在n次试验中，事件A出现的次数应为nP(A)，事件B出现的次数应为nP(B)。又因事件A与B不能同时出现，故在n次试验中，A或B任意一个出现的次数为：nP(A)+nP(B)，因而

P(A+B)=P(A)+P(B)

这个结论推广到互斥的有限个事件，则两两互斥的有限个事件之和的概率等于这些事件的概率之和。用公式表示为：

P(A₁+A₂+……+A_n)=P(A₁)+P(A₂)+……+P(A_n)

A和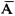构成完备事件组，所以P(A)+P(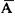)=1。

即任一随机事件A的概率恒等于1减去其对立事件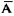的概率。亦即：

P(A)=1－P()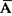

例如，在袋中有20个球，其中白球17个，黑球3个，从中任取3个，求至少有一个是黑球的概率。

解：设事件A为“取出的3个球中至少有一个是黑球”，那么事件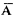为“取出的3个球全是白球”，显见，A与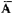互斥，由于

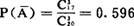
故

P(A)=1－P(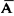)=1－0．596=0．404