排队系统的费用模型

---

在排队系统中，为了减少顾客的等待时间，以减少等待费用，需要提高服务水平，但这却增加了服务机构的成本，二者之间互相矛盾。

为此，建立一个与服务水平有关的费用函数，在服务费用和顾客的等待费用之和为最小的原则下，确定最优服务水平。以M／M／1排队模型为例，设C₁为单位时间内服务水平μ提高一个单位的费用；C₂为顾客等待单位时间的费用；λ为顾客到达率。则单位时间内系统的期望总费用C(μ)及其最优解为：

C(μ)=C₁μ+C₂L_l，

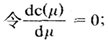
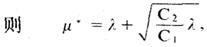
可见，最优解μ^*依赖于。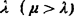

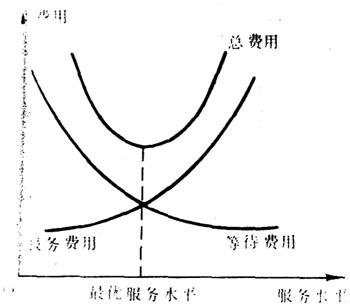
一个排队系统的总费用示意图如下页图：