抛物线法

---

0．618法，分数法，对分法，只需对试验点的试验结果进行比较即可采用。

但这些方法受到试验次数的局限，不能更准确地估计最佳试验点的位置。而抛物线法可以定量描述因素与指标的函数关系，明确指出因素最佳点的位置。

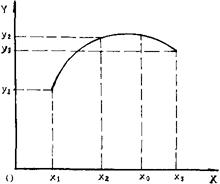
如图所示，设x₁，x₂，x₃三点的试验结果为y₁，y₂，y₃，通过xy平面上的三个点(x₁，y₁)，(x₂，y₂)(x₃，y₃)作二次抛物线

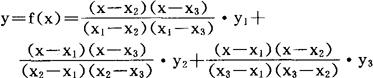
y=f(x)为近似目标函数，通过求极值找到抛物线最大值对应的x₀；

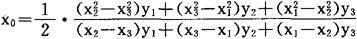
如果x₀不符合要求，则可再选三个点，x₀和x₀附近的X₄，X₅，然后用(x₀，y₀)，(x₄，y₄)，(x₅，y₅)作二次抛物线，求其最优点，如此一直进行下去，到试验结果符合预定要求为止。

抛物线法适用于试验结果呈单峰函数的情况。