如果e1,e2是同一平面上的两个不共线的向量,那么对该平面上的任一向量a,存在惟一的一对实数λ,μ,使a=λe1+μe2.
例1 O是平面上一定点,A、B、C是平面上不共线的三个点,动点P满足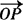 =
=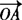 +
+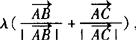 ,λ∈[0,+∞),则P的轨迹一定通过△ABC的( ).
,λ∈[0,+∞),则P的轨迹一定通过△ABC的( ).
分析 (1)设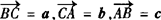 .
.
∵A、B、C三点构成一个三角形,
∴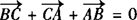 ,即a+b+c=0,只要将
,即a+b+c=0,只要将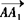 ,
,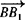 ,
,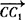 用a,b,c向量表示即可.
用a,b,c向量表示即可.
(2)将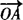 ,
,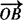 ,
,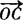 分别用
分别用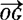 ,
,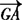 ;
;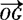 ,
,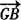 ;
;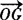 ,
,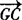 表示出来,得:
表示出来,得:
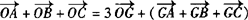 .
.
再证明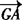 +
+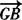 +
+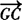 =0即可.
=0即可.
解:(1)∵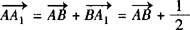
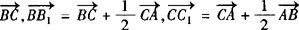 ,∴
,∴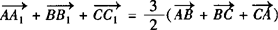 .
.
∵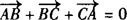 ,∴
,∴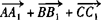 =0.
=0.
(2)∵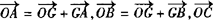
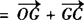 ,
,
∴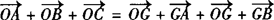
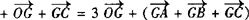 .
.
设D为BC之中点,延长AD至F,使|GD|=|DF|.
∵|BD|=|DC|,
∴四边形BGCF为平行四边形.
∴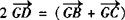 .
.
∵点G为△ABC的重心,∴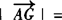
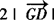 .
.
∴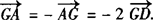 .
.
∴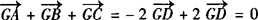 .
.
∴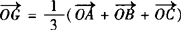 .
.
- (1)电影种类是什么意思
- (1)电影院是什么意思
- (1)电报局是什么意思
- (1)电报机械是什么意思
- 1.电报系统是什么意思
- 1.电视与电视技术是什么意思
- (1)电视播放是什么意思
- (1)电视播放设备是什么意思
- (1)电视种类是什么意思
- (1)电话局是什么意思
- (1)电话机种类是什么意思
- 1.电话系统是什么意思
- 1.男、女劳动力总量结构是什么意思
- (1)画笔是什么意思
- (1)畜力车是什么意思
- 1.畜牧业是什么意思
- 1.畜牧业产值占农业总产值比重是什么意思
- 1.畜牧业产值大幅度增长,在大农业中的比重不断提高是什么意思
- 1.畜牧业先进技术设备引进是什么意思
- 1.畜牧业技术推广是什么意思
- 1.畜禽疫病得到了控制和消灭是什么意思
- 1.畜禽繁殖是什么意思
- 1.畜禽繁殖技术是什么意思
- 1.疾病种类是什么意思
- 1.病害是什么意思
- 1.病虫害是什么意思
- 1.病虫害防治是什么意思
- 1.病虫害预测预报是什么意思
- (1)登山运动是什么意思
- 1.白兔岭水库是什么意思
- 1.白洋淀渔业是什么意思
- 1. 益阳市是什么意思
- 1. 盐城市是什么意思
- 1.盐渍土改良是什么意思
- 1.盘锦河蟹是什么意思
- 1 盘问兄弟说话是什么意思
- 1. 目录电价是什么意思
- (1) 直称是什么意思
- 1相是什么意思
- 1.省内现行柞蚕品种是什么意思
- 1.省内销售是什么意思
- 1.省柴节能大有潜力是什么意思
- 1.省级管理机构是什么意思
- 1.省级综合农业区划研究成果是什么意思
- 1.短暂的繁荣与潜伏的危机是什么意思
- 1. 石家庄市是什么意思
- 1.石油化工生产是什么意思
- 1.石油地质是什么意思
- (1)石油工程是什么意思
- (1)石油的生成是什么意思
- 1.石泉水电站是什么意思
- 1.矿业资源是什么意思
- (1)矿山类型是什么意思
- (1)矿物种类是什么意思
- 1.砂页岩是什么意思
- 1.砂黄土是什么意思
- (1)砖瓦厂是什么意思
- 1.碾米机是什么意思
- (1)磨坊是什么意思
- (1)礼貌是什么意思