随机占优
随机占优stochastic dominance
比较两个风险资产哪一个较优的一种方法。在一个有n种状态的市场上,状态i发生的概率为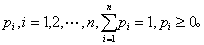 一个风险资产c用一个状态—财富向量c=(c1,c2,…,cn)表示,其中ci是状态i发生时,风险资产c的财富。设还存在另一个风险资产d=(d1,d2,…,dn)。一个投资者的偏好由效用函数v(·)表示,如果
一个风险资产c用一个状态—财富向量c=(c1,c2,…,cn)表示,其中ci是状态i发生时,风险资产c的财富。设还存在另一个风险资产d=(d1,d2,…,dn)。一个投资者的偏好由效用函数v(·)表示,如果
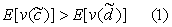
 比
比 好。
好。 和
和 的积累概率分布函数分别为F(e)=Pr{
的积累概率分布函数分别为F(e)=Pr{ ≤e}和G(e)=Pr{
≤e}和G(e)=Pr{ ≤e},它们的概率密度函数分别为f(e)=F′(e)和g(e)=G′(e)。则(1)式等价于
≤e},它们的概率密度函数分别为f(e)=F′(e)和g(e)=G′(e)。则(1)式等价于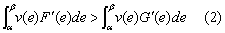
 和
和 取值的下、上限、易于看出,如果下列条件成立:
取值的下、上限、易于看出,如果下列条件成立:
F(e)≤G(e),对所有e∈[α,β] (3)
F(ej)
则当v(·)是增函数时,(1)式必成立,即投资者认为
 优于
优于 。当条件(3)成立时,就称c一阶随机占优于d。条件 (3)从图形看,相当于对任何一个e,F (e) 的图形总位于G(e) 的下方。
。当条件(3)成立时,就称c一阶随机占优于d。条件 (3)从图形看,相当于对任何一个e,F (e) 的图形总位于G(e) 的下方。当曲线F(e)和G(e)有交点且相互穿过时,条件(3)不成立。但若下列条件成立:
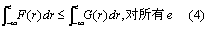
F(ei)≠G(ei),对某一个ei
则当v′>0及v″<0时,(1)式必成立。当条件(4)成立时,称
 二阶随机占优于d。
二阶随机占优于d。☚ 非标准分析 阿罗-德布鲁证券 ☛
- 高原肺水肿是什么意思
- 高原脑水肿是什么意思
- 高原芥是什么意思
- 高原荨麻是什么意思
- 高原血压异常是什么意思
- 高原行脚是什么意思
- 高原裸裂尻鱼是什么意思
- 高原训练是什么意思
- 高原试验是什么意思
- 高原适应不全症是什么意思
- 高原适应不全症混合型是什么意思
- 高原适应锻炼是什么意思
- 高原部队是什么意思
- 高原部队营养是什么意思
- 高原陵是什么意思
- 高原霸王是什么意思
- 高原黑珍珠是什么意思
- 高原鼠兔是什么意思
- 高厦是什么意思
- 高厲是什么意思
- 高去寻是什么意思
- 高县是什么意思
- 高县志是什么意思
- 高县晟是什么意思
- 高县(庆符镇)是什么意思
- 高参是什么意思
- 高参上人是什么意思
- 高又明是什么意思
- 高叉叉是什么意思
- 高友唐是什么意思
- 高友工是什么意思
- 高友朗咏乐其中,行住四仪皆道意。是什么意思
- 高双成是什么意思
- 高反差乳剂是什么意思
- 高反差显影液是什么意思
- 高反差相纸是什么意思
- 高发是什么意思
- 高发人群是什么意思
- 高发区是什么意思
- 高叔嗣是什么意思
- 高叔安是什么意思
- 高取高拔是什么意思
- 高叠于盘中的蔬果是什么意思
- 高古是什么意思
- 高古不称时,沈默岂相竞。是什么意思
- 高古城是什么意思
- 高古奇横,三唐无与抗手是什么意思
- 高句丽是什么意思
- 高句丽—百济战争是什么意思
- 高句丽与公孙氏的争夺是什么意思
- 高句丽与前燕争夺辽东之战是什么意思
- 高句丽乐是什么意思
- 高句丽云梯是什么意思
- 高句丽伐藻那之战是什么意思
- 高句丽侵乐浪带方之战是什么意思
- 高句丽内属是什么意思
- 高句丽农业是什么意思
- 高句丽刀是什么意思
- 高句丽助攻慕容廆之战是什么意思
- 高句丽南北二道是什么意思