质数定理zhishu dingli

关于质素分布的一个定理.令π(x)表示不超过x的质数的个数.例如π(10)=4,π(20)=8,π(100)=25.质数定理是指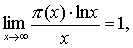：或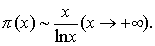这是数论中最著名的定理之一.这一定理是勒让德大约在1800年提出的，在1896年始由阿达玛和达拉瓦勒布桑各自独立地给出了证明，他们的证明使用了高深的整函数理论.后来于1949年由爱多士和薛尔伯格彼此独立地给出了质数定理的初等证明(这里初等证明是指至多用一些初等微积分，但不使用复变函数论方法).
由质数定理容易推出下面的结果：设pn是第n个质数(例如p₁＝2,p₂＝3,p₃＝5等)，则pn～nlnn,(当n→∞).