贝叶斯法则Bayesian Law
亦称“贝叶斯定理”,或称“贝叶斯规则”。在概率统计应用中,对有关概率分布的主观判断进行修正的标准方法。当分析样本大到接近总体数时,样本中事件发生的概率将接近于总体中事件发生的概率。法则广泛应用于经济学领域,用来评价经济学家假设模型、估计经济参数值、预测尚未观察到的变量值。
贝叶斯法则
一种根据新信息修正先验概率,从而得到后验概率的基本方法。这一方法是以英格兰概率统计学家贝叶斯(Bayes,Thomas,1702—1761)的名字命名的。当面临不确定性时,人们对某种事情发生的可能性先有一个先验判断,然后再根据新的信息修正这个判断。在概率论中,修正之前的判断称为“先验概率”,它一般是主观概率判断;根据新信息修正以后的判断称为“后验概率”。假设某种决策有n个可能的结果: A1, A2, …, Ai, …, An,这些结果是独立分布的。假设决策人认为结果Ai发生的先验概率为p(Ai)≥0, ∑ni=1p(Ai)=1。假设事件E能且只能与结果A1, A2, …, Ai, …, An之一同时发生。设在结果Ai发生的条件下,事件E也发生的条件概率为p(E/Ai)≥0, ∑ni=1p(E/Ai)=1,那么事件E发生的概率为:
p(E)=∑ni=1p(E/Ai)p(Ai)
在概率论中,这称为“全概率公式”。用p(Ai/E)表示后验概率,即事件E发生的情况下结果Ai出现的概率。结果Ai和事件E同时出现的联合概率p(Ai,E)满足:p(Ai,E)=p(Ai/E)p(E)
=p(E/Ai)p(Ai)
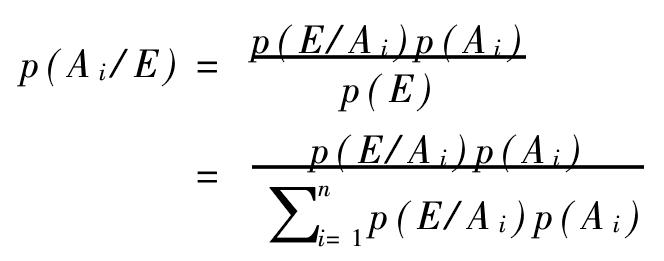
- 孙正容是什么意思
- 孙正气是什么意思
- 孙正阳是什么意思
- 孙步康是什么意思
- 孙武是什么意思
- 孙武令是什么意思
- 孙武先诫是什么意思
- 孙武兵法是什么意思
- 孙武因势用兵是什么意思
- 孙武女兵是什么意思
- 孙武子兵法是什么意思
- 孙武子擂炮兴兵是什么意思
- 孙武子教女兵——十捉八九着是什么意思
- 孙武子教女兵,十捉八九是什么意思
- 孙武用兵是什么意思
- 孙武税收思想是什么意思
- 孙武粉阵试兵法是什么意思
- 孙武练兵,军令如山是什么意思
- 孙武训宫女是什么意思
- 孙武试兵法是什么意思
- 孙武霞是什么意思
- 孙歪头是什么意思
- 孙段村是什么意思
- 孙殿卿是什么意思
- 孙殿安是什么意思
- 孙殿才是什么意思
- 孙殿英是什么意思
- 孙殿起是什么意思
- 孙毅是什么意思
- 孙毅庵奏议是什么意思
- 孙母是什么意思
- 孙毓是什么意思
- 孙毓修是什么意思
- 孙毓堃是什么意思
- 孙毓敏是什么意思
- 孙毓棠是什么意思
- 孙毓汶是什么意思
- 孙毓溎是什么意思
- 孙毓熊是什么意思
- 孙毓筠是什么意思
- 孙毓芹是什么意思
- 孙氏是什么意思
- 孙氏兄弟争受戮案是什么意思
- 孙氏医书三种是什么意思
- 孙氏医学三种是什么意思
- 孙氏医学丛书是什么意思
- 孙氏医案是什么意思
- 孙氏古文是什么意思
- 孙氏周易集解是什么意思
- 孙氏太极剑对练是什么意思
- 孙氏太极拳是什么意思
- 孙氏太极拳剑是什么意思
- 孙氏成败志是什么意思
- 孙氏打胎身死案是什么意思
- 孙氏殉夫是什么意思
- 孙氏百日咳验方是什么意思
- 孙氏祠堂书目是什么意思
- 孙民是什么意思
- 孙水是什么意思
- 孙水河是什么意思