等级相关

将两个变量的观察值分别用它们的等级(即从小到大的序号，亦称秩)来表示，研究等级间的相关。常被应用于测验分数统计中。

等级相关dengji xiangguan

又称秩次相关。当两列变量的分布形态不明确且变量数小于30，或两列变量为等级变量时，计算这两列变量之间的相关要用等级相关。公式如下：

式中D为二列对偶等级的差数，∑D²是各D的平方之和，N为等级的数目。当计算多列等级相关时，要用肯德尔和谐系数来表示。

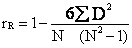
等级相关rank correlation

是非参数分析方法之一，亦称秩相关。将两组有关指标按大小顺序排列并划定等级，而后判断其间的相关关系。常用者有Spearman法和Kendall法两种。

等级相关rank correlation

用等级 （顺序） 变量计算两组变量间的相关程度，常用的有二个系数，一个是斯皮尔曼的ρ，另一个是肯达尔的τ。设X和Y的n对观察值为(x_i,y_i),i=1,2，…，n，将x₁，…，x_n按由小到大（或由大到小）的顺序排列，用排列后的位次来代替变量值，即x_i所对应的等级。同样用y_i对应的等级代替其变量值。斯皮尔曼等级相关系数ρ的公式为：

其中，x_i和y_i均为相应等级。如果设d_i＝x_i-y_i,i=1,2，…，n，则等级相关系数可简化为： ρ=1-
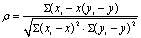
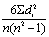
肯达尔系数τ的公式为

其中C表示n对变量中取出的两两排列的对其中排列顺序相一致的总对数，D表示排列顺序不一致的总对数，n对变量两两比较共有(n/2)=n(n-1)/2对，因此C+D=n (n-1)/2。以上两个系数的取值也在-1与1之间。

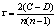
等级相关

研究两个等级排列序列之间相关的程度。有时，研究对象无法以精密数量确定其大小，但可以依次排列其等次（或等级）。同一研究对象的两种 （或两个）等级排序数列，是否相关，相关程度如何，可以用等级相关系数：

来度量。式中，D指两个等级数列中每对项目间等级之差； N是等级数目。ρ的性质，与相关系数类似。

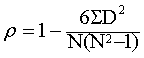
等级相关grade correlation

研究两个等级排列序列之间相关的程度。有时，研究对象无法以精密数量确定其大小，但可以依次排列其等次（或等级）。同一研究对象的两种（或两个）等级排序数列，是否相关，相关程度如何，可以用等级相关系数：

来度量。式中，D指两个等级数列中每对项目间等级之差；N是等级数目。ρ的性质，与相关系数类似。

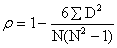
等级相关

等级资料的直线相关分析称等级相关，这是一种非参数统计方法。分析两事物数量间的直线关系时，对下列情况宜用等级相关：
❶两事物的量，有的不能准确测量，只能按大小、程度、优劣或综合判断给出顺序号；
❷虽可测量，但总体数据的分布未知或已知不是正态双变量，不能作积差相关分析；
❸只需对两事物数量之间的关系作初步分析等。
等级相关的常用分析方法有Spearman法和Kendall法，两法有很多共同点：
❶都是用一个等级相关系数(分别用符号r_S及rK表示)来说明两变量间直线关系的方向和密切程度。r_S或r_K的值都在+1与-1之间，数值为正表示正相关，数值为负表示负相关。
❷样本r_S及r_K分别是总体等级相关系数ρ_S及ρ_K的估计值，要推断总体中两变量X、Y间有无直线关系须经假设检验。两法的不同点只是r_S及r_K的计算方法不同，作假设检验时的统计用表不同。

表1 等级相关系数rs界值表

n	P(1): 0.05 P(2):0.10	0.025 0.05	0.01 0.02	0.005 0.01
4	1.000
5	0.900	1.000	1.000
6 7 8 9 10	0.829 0.714 0.643 0.600 0.564	0.886 0.786 0.738 0.700 0.648	0.943 0.893 0.833 0.783 0.745	1.000 0.929 0.881 0.833 0.794
11 12 13 14 15	0.536 0.503 0.484 0.464 0.446	0.618 0.587 0.560 0.538 0.521	0.709 0.678 0.648 0.626 0.604	0.755 0.727 0.703 0.679 0.654
16 17 18 19 20	0.429 0.414 0.401 0.391 0.380	0.503 0.485 0.472 0.460 0.447	0.582 0.566 0.550 0.535 0.520	0.635 0.615 0.600 0.584 0.570
25 30 35 40 45	0.337 0.306 0.283 0.264 0.248	0.398 0.362 0.335 0.313 0.294	0.466 0.425 0.394 0.368 0.347	0.511 0.467 0.433 0.405 0.382
50 60 70 80 90	0.235 0.214 0.198 0.185 0.174	0.279 0.255 0.235 0.220 0.207	0.329 0.300 0.278 0.260 0.245	0.363 0.331 0.307 0.287 0.271
100	0.165	0.197	0.233	0.257

摘自 Zar JH: Biostatistical Analysis,p498 Pren-tice-Hall,Inc.,1974

表2 等级相关系数rK界值表

n	P		n	P
	0.05	0.01		0.05	0.01
4 5	1.000 .800	1.000 1.000	21 22 23 24 26	.267 .264 .257 .246 .240	.371 .359 .352 .341 .333
6 7 8 9 10	.733 .619 .571 .500 .467	.867 .810 .714 .667 .600	26 27 28 29 30	.237 .231 .228 .222 .218	.329 .322 .312 .310 .301
11 12 13 14 15	.418 .394 .359 .363 .333	.564 .545 .513 .473 .467	31 32 33 34 35	.213 .210 .205 .201 .197	.295 .290 .288 .280 .277
16 17 18 19 20	.317 .309 .294 .287 .274	.433 .426 .412 .392 .379	36 37 38 39 40	.194 .192 .189 .188 .185	.273 .267 .263 .260 .256

摘自 Daniel WW: Applied Nonparametric Statis-tics,p467,Houghto Mifflin Company,1978
Spearman法 等级相关系数rS的计算步骤如下：(1)将成对的资料列出如表3第(2)、(4)栏。如果原资料不是秩次，则X、Y分别按数量从小到大编秩，如表3第(3)、(5)栏。例如公社4黄曲霉素相对含量为0.7，是10个公社中最低的，定秩次为1；稍高的是公社2，相对含量为1.0，定秩次为2；余类推。若几个观察值相等，应将它们的秩次相加求平均秩次，作为每个观察值的秩次。如果公社4、2的相对含量皆为0.7，那么它们的秩次均应定为1.5[=(1+2)/2]。
(2)计算每对观察值秩次的差值d及d₂、∑d₂，如表3第(6)、(7)栏。
(3) 按式(1)计算r_S。

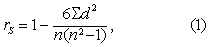
式中n为样本含量。
对r_S进行ρ_s＝0的假设检验，只需将算得的r_S按n查表1(r_S界值表)得P值，按所取检验水准作出推断结论。
例1 肝癌病因研究中，调查某地10个公社的肝癌死亡率(1/10万)Y，与某种食物中黄曲霉毒素相对含量(以最高含量为10)X，结果见表3第(2)、(4)栏。试用Spearman等级相关系数推断X、Y间有无直线相关。
H₀: ρs =0,
H₁: ρs≠0,a=0.05。
编秩及初步计算结果见表3第(3)、(5)、(6)、(7)栏。

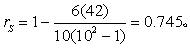
按n=10查表1得P=0.02，按a=0.05水准拒绝H₀，接受H₁。可以认为食物中黄曲霉毒素含量与肝癌死亡率间有正相

表3 rS计算表

公社 编号 (1)	黄曲霉毒素相对含量		肝癌死亡率(1/10万)		d (6)	d2 (7)
	X (2)	秩次 (3)	Y (4)	秩次 (5)
1 2 3 4 5 6 7 8 9 10	3.7 1.0 1.7 0.7 4.0 5.1 5.5 5.7 5.9 10.0	4 2 3 1 5 6 7 8 9 10	46.5 18.9 14.4 21.5 27.3 64.6 46.3 34.2 77.6 55.1	7 2 1 3 4 9 6 5 10 8	-3 0 2 -2 1 -3 1 3 -1 2	9 0 4 4 1 9 1 9 1 4
						42

关。黄曲霉毒素含量高，肝癌死亡率也高。
r_S的校正： 编秩时，观察值相同则取平均秩次，但相同秩次较多时，影响Σd₂值，这时可用式(2)计算校正等级相关系数r′S。

次的个数。k为有相同秩次的组数.当TX=TY=0时，式(2)等于式(1)。
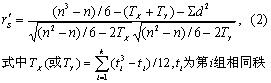
假定例1中前5个公社的X相同，各取平均秩次为3；第6、7、8公社的X相同，各取平均秩次为7；第9、10公社的X也相同，各取平均秩次为9.5。这样k=3,t₁＝5，表示5个秩次相同，同理t₂＝3,t₃＝2。故T_X＝(53-5)/12+(3^3-3)/12+(23-2)/12=12.5。肝癌死亡率没有相同秩次，故T_Y＝0。并算得Σd₂＝33.5。计算校正的等级相关系数为

若不校正，将Σd²＝33.5代入式(1)，得r_S＝0.797。Kendall法 等级相关系数rK的计算步骤如下：
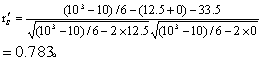
(1) 列资料，编秩次，同Spearman法，并要求将其中X或Y的秩次按自然数排列，如表4第(2)、(3)栏。
(2) 计算累计秩次个数S。若X的秩次按自然数排列，则计算Y的每个秩次下面大于该秩次的秩次个数，然后合计即S。如表4第(4)栏。Y的第1个秩次为3,3的下面9个秩次中比3大的有7个，故秩次个数为7; Y的第4个秩次为7，其下大于7的秩次个数为3，余类推。这些Y的累计秩次个数合计为34即S。
当遇到原始数据相同时，仍取平均秩次，按下例求累计秩次个数。

秩 次		Y的累计 秩次个数 5 3 3 1 1 0
X 1 2 3 4.5 4.5 6	Y 1 2.5 2.5 4 5 6

Y的第一个秩次是1，其下有5个比它大，故秩次个数为5; Y的第二个秩次为2.5，下面有3个比它大，故秩次个数为3;Y的第四个秩次为4，与它对应的X秩次是4.5，它下面的一个秩次也是4.5，所以第4个秩次个数记为1而不是2。这样处理的依据是，当分析X与Y的相关时，X变Y不变或X不变Y变，均属无相关。
(3) 按式(3)计算r_K值。

式中n为样本含量。
对r_K进行ρ_K＝0的假设检验，只需将算得的r_K按n查表2(r_K界值表)得P值，再按所取检验水准作出推断结论。
r_k的校正： 当相同秩次较多时，可用下式计算校正等级相关系数r'K

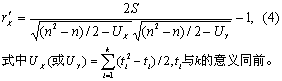
例2 试对例1资料用Kendall等级相关系数作分析。

表4 rK计算表

公社编号 (1)	秩 次		Y的累计 秩次个数 (4)
	黄曲霉毒素相 对含量，X (2)	肝癌死亡率 (1/10万),Y (3)
4 2 3 1 5 6 7 8 9 10	1 2 3 4 5 6 7 8 9 10	3 2 1 7 4 9 6 5 10 8	7 7 7 3 5 1 2 2 0 0
			34 (S)

H₀: ρ_K＝0,
H₁: ρ_K≠0。
α=0.05。
将X的秩次按自然数排列并计算Y的累计秩次个数见表4第(4)栏。

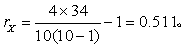
按n=10查表2，得0.05>P>0.01，按α=0.05水准拒绝H₀，结论同例1。

等级相关

又称“斯皮尔曼等级相关”。是英国统计学家提出的用于计算定序变量间相关关系的方法。在计算两种变量相关时，等级相关法只考虑各变量在数列中所在的位置，不问其绝对值的大小。因为它是按照各变量在数列中所在等级位置的顺序计算的，所以又称之为等级顺序相关系数，通常用ρ表示(ρ读Rho)。当数据资料无法用定距或定比变量表示时，对于定序变量(如赞同程度、文化程度等)间的相关关系，通常用等级相关法加以测定。其相关系数的计算公式为：ρ=1-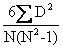。式中，D为X与Y变量等级的差数，N为总次数。

等级相关rank correlation

测量变量之间的单调关系的强度的一种统计方法，亦称“秩次相关”。在统计中，往往有许多现象或变量并不全用数量表示，而是用等级来表示的。例如某些心理过程的品质不宜用分数量尺来测定，在这种情况下，要求得两种心理活动品质的相互关系，就必须采用等级相关法。等级相关法是英国统计学家斯皮尔曼(Spearman,C.E.)提出的，其计算公式为：

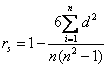
式中r_s为等级相关系数，d为每两个对应等级之差数，n为成对数据的个数。等级相关适用十小样本的测量数据(一般在10～30之间)的相关分析。如果等级相同的量数过多时，则根据等级所得的结果过大，不如用积差法求得结果精确。