电通量diantongliang

描述作为矢量场的电场性质而引入的物理量。在电场中取一面元ds，以n表示其法线方向的单位矢量，则ds=nds叫做矢量面元，若面元处的场强为E，定义E·ds=dΦE(或dΦE=Ecosθds)，叫做面元ds的电通量。对于有限曲面而言，其电通量是将曲面上所有面元电通量相加而得出的，即

对闭曲面的电通量

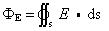
在一定意义下，电通量等于通过该面（有限曲面或闭合曲面）电力线的条数，通量是描写矢量场的重要物理量。电场是矢量场的一种，如果全部空间或部分空间的每 一点都对应着某个矢量的一个确定值，就说该空间为该矢量的矢量场，例如稳恒流体中每一点都有一个确定的流速v(x、y、z)，则所研究的流体空间为v(x、y、z)矢量场；电场中每点都有一个确定的电场强度矢量E(x、y、z)，则电场为E(x、y、z)矢量场；同理磁场为磁感应强度B(x、y、z)的矢量场。凡是矢量场都可以定义该矢量的通量，并由任意闭曲面的通量性质来区分该矢量场的性质。在矢量场A(x、y、z)中，若面元dS处的矢量为A，则定义dΦA=A·ds为面元dS的A通量。有限曲面的A通量ΦA=A ds，闭曲面的A通量ΦA=A·ds。对稳恒流速场dΦ_v＝v·ds，对电场dΦA=E·ds…等等。通量是代数量，有正有负。当ds=nds的法线矢量n与场强E(或流速v)的夹角θ为锐角时，dΦ_k＝Ecosθds>0(或dΦ_v＝vcosθds>0)；当θ为钝角时，dΦE=Ecosθds<0(或dΦ_v＝vcosθds<0)；当θ=90°时，dΦE=0(或dΦv=0)。对有限曲面（包括闭曲面）的通量也是如此。一个曲面有正、反两面，与此对应，它的法线矢量有正、反两种取法。对单个面元或不闭合曲面，法线矢量的正反取向是无关紧要的。但闭合曲面则把整个空间分成内、外两个部分，其法线矢量指向曲面外部空间的叫外法线矢量，指向曲面内部空间的叫内法线矢量。当涉及矢量场的通量的讨论时，我们规定：对于闭合曲面，总是取它的外法线矢量为该处的法线方向。（电）通量可以迭加。若E=E₁+E₂，则通过某曲面S的（电）通量为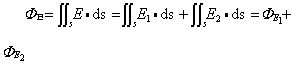

有些矢量场的通量有明显的物理意义，例如稳恒流速场中，通量dΦv=v·ds=vcosθds，等于单位时间内流过面元ds的流体体积。若该流体的密度为1，通量dΦv等于单位时间内流过ds的流量。电通量没有明显的物理意义，但电磁学中，通常规定通过面元ds的电力线条数dN等于面元电通量dΦE，因而

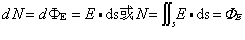
这样，穿过某曲面的电通量就是穿过该曲面的电力线条数，若N>0，就说电力线从面内穿出；N<0，说电力线从面外进入。前面提到，由任意闭曲面的通量性质来区分该矢量场的性质。广义的说，若矢量场A(x、y、z)对任意闭曲面都满足sA·ds=0，称该矢量场为无源场；若存在sA·ds > 0，称闭曲面内有正源；若存在sA·ds< 0，称闭曲面内有负源。总之，若存在闭曲面的通量不等于零，就说该矢量场是有源场。高斯定理说明对任意闭曲面的电通量为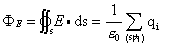

故静电场是有源场，电荷就是源头。若已知某曲面（平面为其特例）上场强E的值相等，且E平行或反平行于n，且求出该曲面的电通量Φ，则由Φ=ES求得面上的E，若E平行于n，则E=Φ/Sn，场强E沿该点的法线方向；若E反平行于n,E=-Φ/Sn,E与该点面元法线方向反向。

电通量

“电位移通量”的简称。

电通量

electric flux