特征函数characteristic function

设F_ξ(x)是随机变量ξ的分布函数，称函数

φ(t)=E(e^itξ)=∫^+∞_-∞e^itxdF_ξ(x)
(-∞
为随机变量ξ的特征函数。如果ξ为连续型的，它的密度函数为f(x)，则它的特征函数为φ(t)=E(e^itξ)=∫^+∞_-∞e^itxf(x)dx；如果ξ是离散型的，它的分布列为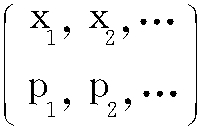，则它的特征函数为φ(t)=E(e^itξ)=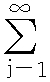e^itx_jp_j。在一般情况下，数学期望、方差只能粗略地反映分布函数的某些性质，能够完全刻画分布函数的是它的特征函数。特征函数有时比分布函数更便于应用。