消费者需求基本矩阵方程Consumer Demand Basic Matrix

假定效用函数u(x)是二次连续可微分的， x∈X是消费丛，需求函数(p,w)定义为
(p,w)={x∈X px≤w，若px′≤W则x=x′或非x′=x}
其中价格p和财富w是预先给定的.那么经典最大化问题max{u(x)x∈X,px=w}的解就是x⁰＝(p,w)。考虑对应的拉格朗日函数，由极值的一阶条件得到

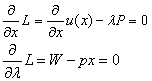
对应于解x⁰＝(p,w)，可以解出λ的解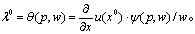用U表示u的海赛矩阵，U⁰为U在x⁰＝(p,w)的值，一阶条件就化为
U⁰dx-λ⁰dp-pdλ=0
dw-pdx-x ⁰dp=0
写成矩阵形式就是

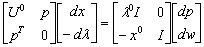
其中I是单位矩阵(K阶)，这就是消费者需求基本矩阵方程。