正则连分数
正则连分数zhengze lianfenshu
有限连分数
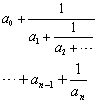
| 或无限连分数 |
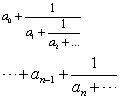
任一个有限正则连分数,只要从最下面开始逐步化简,总能化成一个正有理分数p/q(p,q ∈N).故知有限正则连分数表示一个正有理分数.反之,任何一个正有理分数总可通过辗转相除的方法化为一个有限连分数,例如
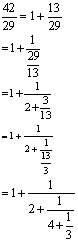
对于无限正则连分数,不难用数学归纳法证出它的各个渐近分数pn/qn满足关系式:n≥2时
| pn=anpn-1+pn-2, qn=an·qn-1+qn-2 |
| 其中q0=1,p0=a0,q1=a1,p1=a0a1+1 |
| 由此可得 |
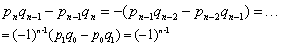
| 进而又可导出 |
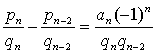
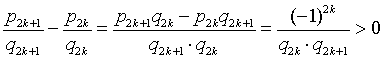
| 结合上段所述即知 |
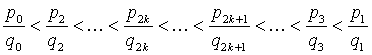
| 再注意到对任何n∈N,qn≥n,知 |
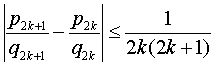
| 所以 |
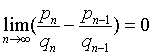
于是根据区间套定理知:
 pn/qn存在,即正则连分数一定收敛.由于有理数必能化成有限正则连分数,故无限正则连分数之值必是无理数.例如
pn/qn存在,即正则连分数一定收敛.由于有理数必能化成有限正则连分数,故无限正则连分数之值必是无理数.例如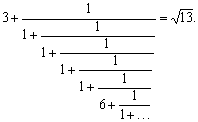
可以证明:无限正则连分数的各个渐近分数中,n越大的与连分数的真值之差距越小.一般把初项a0叫做这个连分数的一阶渐近分数,pn/qn就相应地叫做第n+1阶渐近分数.
还可以证明:无限正则连分数的任一渐近分数pn/qn,在分母不超过qn的一切有理即约分数中是最接近连分数真值的.
☚ 连分数 循环连分数 ☛
- 肥料使用是什么意思
- 肥料保证成分是什么意思
- 肥料分析式是什么意思
- 肥料利用率是什么意思
- 肥料利用率示踪测定是什么意思
- 肥料副成分是什么意思
- 肥料后效是什么意思
- 肥料品位是什么意思
- 肥料堆是什么意思
- 肥料学是什么意思
- 肥料实用技术参考手册是什么意思
- 肥料对环境的污染是什么意思
- 肥料手册是什么意思
- 肥料挂帅是什么意思
- 肥料换谷制度是什么意思
- 肥料撒施量是什么意思
- 肥料效应是什么意思
- 肥料效应函数是什么意思
- 肥料效应函数法是什么意思
- 肥料效应曲线是什么意思
- 肥料效应曲面是什么意思
- 肥料有效性示踪研究是什么意思
- 肥料有效成分是什么意思
- 肥料树是什么意思
- 肥料检测实用手册是什么意思
- 肥料残效是什么意思
- 肥料残效示踪研究是什么意思
- 肥料比率是什么意思
- 肥料混合是什么意思
- 肥料添加剂是什么意思
- 肥料的产量效应是什么意思
- 肥料的效力是什么意思
- 肥料盐指数是什么意思
- 肥料等级是什么意思
- 肥料系统是什么意思
- 肥料试验是什么意思
- 肥料试验设计是什么意思
- 肥料调理剂是什么意思
- 肥料载送剂是什么意思
- 肥料配合式是什么意思
- 肥料需要量是什么意思
- 肥有是什么意思
- 肥朗朗是什么意思
- 肥条是什么意思
- 肥杵杵是什么意思
- 肥株子风是什么意思
- 肥桶是什么意思
- 肥梁大腿是什么意思
- 肥楞楞的是什么意思
- 肥母是什么意思
- 肥母鸡是什么意思
- 肥毒是什么意思
- 肥气是什么意思
- 肥气丸是什么意思
- 肥气积一百三十是什么意思
- 肥水是什么意思
- 肥水下塘是什么意思
- 肥水不外流是什么意思
- 肥水不往外边流是什么意思
- 肥水不流外人田是什么意思