概率ɡàilǜ
某类事在相同条件下,发生可能性的量
△ 雾天出车祸的~较高。
概率gài lǜ
随机事件出现的可能性的量度。1958年《新知识词典》“或然率论”条:“或然率论: 也称概率论、机率论,是一种数学的理论。”◇几率、或然率、决疑率、机会律、决疑数、机率。
概率gài lǜвероятность
概率
事件在随机试验中发生的可能性大小的一个数值度量。事件A的概率记为P(A)。必然事件的概率为1,不可能事件的概率为0,任意事件的概率总介于0与1之间。有各种方法可以获得一个事件的概率,譬如在古典概型中,设随机试验具有n(有限)个基本事件,而事件A中含k个基本事件,则P(A)=k/n;又譬如可以把概率看成是频率的稳定值,只要试验次数n充分大,如果在n次试验中事件A出现k次,则可以把k/n看成是事件A的概率的一个估计。常被应用于测验分数统计中。
概率gailu
在客观世界中有许多现象属于随机(偶然)现象,它是在一定条件下具有多种可能结果的现象。如政治课得95分的学生,他可能是“三好”学生,也可能不是“三好”学生;一道4选1的选择题,对不懂该题而凭猜测作答的考生,只能随机挑选其中的1个选项。这种随机现象的每个结果叫作随机事件。一个随机事件在一次操作中可能发生、也可能不发生,我们只能谈论它发生的可能性多大。怎样估计它发生的可能性的大小呢?我们可通过大量操作来估计。设在n次操作中随机事件A发生了m次,则比值m/n就称为随机事件A的频率。可见,任何随机事件的频率均介于0与1之间。
对随机事件A的一次大量操作,就有一个频率,而多次大量操作就有多个频率。这多个频率虽不完全相同,但却呈现出在某个固定值附近摆动的稳定性。因此当操作大量进行时,随机事件A出现的一种稳定频率或频率所接近的极限值就称为事件A发生的概率,即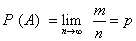
[例] 设全班50个学生中有男生30人、女生20人,则在全班中任选一个学生为男生的概率是30/50=0.6。它是指当大量随机抽选学生的情况下,该班出现男生事件的一种稳定比率,而不是说每抽取5个学生中将有3个男生。
概率有如下性质:
❶任何随机事件A的概率都是一个大于0而小于1的正数,即0≤P (A)≤1;
❷必然(一定发生的)事件的概率为1,不可能(必不发生的)事件的概率为0。
概率gailu
随机事件在一次试验中是否发生,是无法事先肯定或否定的偶然现象。但是,在大量重复试验中,就可能会呈现出一定的规律性。有些事件发生的可能性大些,有些事件发生的可能性小些。我们将刻划随机事件发生的可能性大小的数量指标,称为该事件发生的概率。设随机事件为A,则用P (A)表示事件A发生的概率。
概率Gailu
随机事件发生的可能性大小的度量。在客观世界中有许多现象属于随机现象,它在一定条件下具有多种可能结果,我们事先无法精确预测会出现那种结果。例如我们测量小学生智力,在随机选取一个学生进行测量时,事先并不能确定其智商分数。随机现象的各种结果叫做随机事件。一个随机事件在一次操作中可能出现,也可能不出现,但我们可以确定它出现的可能性。概率即是这种可能性的度量,它是介于0和1之间的实数。如果一个事件概率为1,称为必然事件,不可能事件的概率为0。概率这一概念的意义基于下面这种现象:虽然在一次操作中不能预测某事件A是否发生,但在多次操作中事件A发生的次数与操作总次数之比(即频率)越来越接近某一常数,即
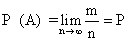
概率
又称“或然率”、“几率”。概率论中最基本的概念。刻划随机事件发生可能性大小的一个量,数值大于或等于0,小于或等于1。
概率
某种事件在相同条件下可能发生也可能不发生,而表示发生的可能性大小的量谓之概率。
概率probability
是表示某事件发生的可能性,通常以P表示。概率值介于0与1之间。P=1的事件,称必然事件,P=0的事件,称不可能事件。P值越大,提示某事件发生的可能性越大。在统计推断中,当某一事件发生的可能性很小时,即可以认为该事件不会发生。
概率Probability
见“或然率”。
概率
衡量随机事件出现的可能性大小的量。参见“随机变量”。
概率
概率是描述事件发生可能性大小的一个度量。事件的概率有不同的规定。概率的古典定义是: 设一个试验的所有可能出现的结果有n个,这些结果是互不相容且等可能的,其中有f个结果具有属性A,则具有属性A的事件(简称事件A,下同)出现的概率记作

P(A)=p。(2)
在许多实际问题中,当概率不易求得时,只要n充分大,可以将频率作为概率的估计值。
在一定条件下,肯定发生的事件称为必然事件,肯定不发生的事件称为不可能事件。可能发生也可能不发生的事件,如未出生的婴儿是女的、某人的血型(未查血型前)是O型等事件,称为随机事件,亦称偶然事件,简称事件。必然事件的概率等于1,不可能事件的概率等于0,随机事件的概率介于0与1之间。
“事件A和B中至少有一个发生”也是一个事件,称此事件为A、B之和或并,记作A+B。“事件A和B同时发生”这一事件称为A、B之积或交,记作AB。例如对某地农民粪检结果,有蛔虫阳性者,钩虫阳性者,钩虫、蛔虫均为阳性者,则“钩虫和蛔虫中至少有一阳性”这一事件称为钩虫阳性与蛔虫阳性这两事件之和;钩虫、蛔虫均为阳性称为这两事件之积。
如果两事件A、B不可能同时发生,就说A、B互不相容。如某人的“血型为O型”或“血型为A型”是互不相容的两事件。如果互不相容的诸事件的概率之和等于1,就说它们构成完备系,例如诸血型构成完备系。当完备系中只有两个互不相容的事件时,就说它们是相互对立的事件,如“血型为O型”与“非O型”是相互对立的事件。事件A的对立事件记作A。两事件A与B的关系可示如图。
概率运算法则
(1) 加法法则: 对于任意两事件A和B中,至少有一个发生的概率为
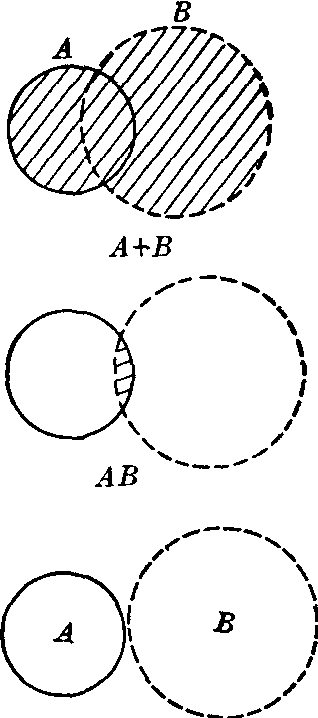
A.B互不相容
A、B两事件关系示意
P(A+B)=P(A)+P(B)-P(AB)。(3)若A、B互不相容,则
P(A+B)=P(A)+P(B)。(4)
式(4)可推广到有限个互不相容的事件。相互对立事件的概率之和等于1,即
P(A)+P(Ā)=1。 (5)
(2)乘法法则: 在“事件A已发生”的条件下,事件B发生的概率称为B的条件概率,记作P(B|A)。对于任意两事件A和B同时发生的概率为
P(AB)=P(A)P(B|A),
或 P(AB)=P(B)P(A|B)。(6)
若A(或B)发生与否并不影响B(或A)的概率,就说A与B相互独立,这时P(B|A)=P(B)或P(A|B)=P(A)。若事件A与B相互独立,则事件AB的概率等于A的概率与B的概率之积,即
P(AB)=P(A)·P(B)。(7)
这一法则可推广到有限个相互独立的事件。
例1 某单位检查全体人员1500人的寄生虫病,结果: 80人有蛔虫病,30人有钩虫病,15人兼有蛔虫病和钩虫病。设“患蛔虫病”为事件A,“患钩虫病”为B,求P(A+B)及P(AB)。以频率作为概率,按式(3)
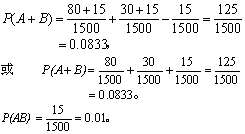
例2 已知某地区人群血型分布的频率: O型为36%,A型为28%,B型为28%,AB型为8%,求该地区某人不是O型的概率。
诸血型构成完备系,故
P(A型)+P(B型)+P(AB型)+P(O型)=28%+28%+8%+36%=1。
因此,按式(4)得
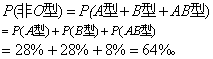
本例的另一解法是,按式(5)得
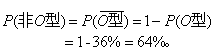
例3 设有一群同种属、同月龄、同性别的大白鼠注射某种药物,经一定时间后,其死亡率为0.60。今从中随机抽取4只注射该药物,求此4只中有3只死亡的概率。
假定任一鼠注射后死亡与否对他鼠并无影响,即各鼠的“死亡”事件是相互独立的。设四鼠分别以A、B、C、D表示,则三死一生有下列四种情况:
| 死 | 死 | 死 | 生 | |
| 1 | A | B | C | D |
| 2 | D | A | B | C |
| 3 | C | D | A | B |
| 4 | B | C | D | A |
每一种情况发生的概率,按式(7)均为
(0.6)3(1-0.6)=(0.6)3(0.4)=0.0864,
而这四种情况是互不相容的,故应将四个0.0864相加,于是按式(4)得
P(三死一生)=4(0.6)3(0.4)=0.3456。
Bayes公式 设H1,H2,…,Hn为n个不相容的事件,并且构成完备系,P(Hi)>0(i=1,2,…,n);则在事件A出现的条件下,事件Hi出现的概率,即Hi的条件概率为
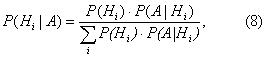
例4 某地区根据多年的某种病史分析,将病例分为甲状腺机能低下(H1)、正常(H2)与亢进 (H3) 三类,并得: P(H1)=0.15,P(H2)=0.65,P(H3)=0.20。若仅按“食欲亢进”指标(A)而言,根据积累的资料得: P(A|H1)=0.08,P(A|H2)=0.10,P(A|H3)=0.61。今有某病员新近食量大增,试分别求其甲状腺机能低下,正常与亢进的概率。
按式(8)得
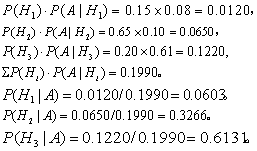
故仅按“食欲亢进”一项指标而言,该病员患甲状腺机能亢进的可能性最大,约2倍于正常,10倍于低下。
概率
表示在社会和自然界中某一类事件在相同条件下可能发生也可能不发生(这类事件称随机事件),发生可能性大小的一个量。数学概率论中最基本的概念。也称或然率、几率。概率论规定:必然发生的事件的概率为1,不可能发生的事件的概率为0,而一般的随机事件的概率必介于0与1之间的一个数。概率值越大,该事件发生的可能性就越大。
概率
亦称“或然率”、“机率”。它反映随机事件出现的可能性大小的量度。随机事件是指在相同条件下,可能出现也可能不出现的事件。例如,从一批有正品和次品的商品中,随意抽取一件,“抽得的是正品”就是一个随机事件。设对某一随机现象进行了n次试验与观察,其中A事件出现了m次,即其出现的频率 为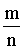 。经过大量反复试验,常有
。经过大量反复试验,常有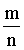 越来越接近于某个确定的常数。该常数即为事件A出现的概率,常用P (A) 表示。概率有如下基本性质:(1) 任一随机事件A出现的概率P (A) 总是介于0与1之间: 0≤P (A) ≤1; (2) 必然出现的事件U的概率等于1,即P (U) =1; (3) 不可能出现的事件V的概率等于零,即P (V) =0。概率越大,表示事件出现的可能性越大。这是从统计的角度来定义概率的,可称之为统计概率。
越来越接近于某个确定的常数。该常数即为事件A出现的概率,常用P (A) 表示。概率有如下基本性质:(1) 任一随机事件A出现的概率P (A) 总是介于0与1之间: 0≤P (A) ≤1; (2) 必然出现的事件U的概率等于1,即P (U) =1; (3) 不可能出现的事件V的概率等于零,即P (V) =0。概率越大,表示事件出现的可能性越大。这是从统计的角度来定义概率的,可称之为统计概率。
概率probability
随机事件发生的可能性大小的度量,亦称“或然率”、“几率”,是概率论中最基本的概念。统计学中常用符号P表示概率。P(A)就是随机事件A发生的概率。把必然发生的事件的概率规定为1,不可能发生的事件的概率规定为0,则概率的性质: (1)事件A的概率不小于0,不大于1, 即0≤P(A)≤1。(2)必然事件的概率等于1。(3)不可能发生的事件的概率为0。(4)如果事件A出现的概率为P(A), 则A 的对立事件(即A不出现)的概率为:P()=1-P(A),如果A事件出现的概率写作P,不出现的概率写作q,则q=1-p,或P+q=1。事件发生的概率接近于1,表明该事件发生的可能性越大,愈接近于0,则表明发生的可能性越小。
概率probability
亦称“几率”、“或然率”。表示随机事件出现可能性大小的客观指标。用P(A)表示。数值大小在0与1之间。是事件本身所固有的不随人的主观意愿而改变的一种属性,经过大量观测之后,概率的规律性将凸显出来,如正态分布等。分为后验概率和先验概率。后验概率,指在对随机现象进行n次观测时,其中某一事件A出现的次数m与观测次数n的比值,随着n→∞时,它将稳定在一个常数P上,这一常数称为概率。先验概率,指随机现象的所有可能结果(称为基本事件)是有限的,其数量为n,每一个基本事件发生的可能性相同,事件A包含m个基本事件,事件A的概率为P(A)=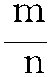 。
。
概率
亦称“几率”、“或然率”,表示随机事件出现可能性大小的客观指标。是概率论研究的主要内容。用字母P表示。分为后验概率和先验概率。后验概率,指在对随机现象进行n次观测时,其中某一事件A出现的次数m与观测次数n的比值,随着n→∞时,它将稳定在一个常数P上,这一常数即概率。由于这种概率由事件A出现的次数决定,所以称为“后验概率”或“统计概率”。先验概率,亦称“古典概率”,指随机现象的所有可能结果(称为基本事件)是有限的,其数量为n,每一个基本事件发生的可能性相同,事件A包含m个基本事件,事件A的概率为P(A)=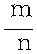 。
。
- 玉麟是什么意思
- 玉麟堂帖是什么意思
- 玉麟符是什么意思
- 玉麟记是什么意思
- 玉麟香腰是什么意思
- 玉麦是什么意思
- 玉麦包包是什么意思
- 玉麦子子是什么意思
- 玉麦核核是什么意思
- 玉麦根根是什么意思
- 玉麦桩桩是什么意思
- 玉麦泡是什么意思
- 玉麦疙蔸是什么意思
- 玉麦秸是什么意思
- 玉麦粑粑是什么意思
- 玉麦花是什么意思
- 玉麦花儿是什么意思
- 玉麦花花是什么意思
- 玉麦镬镬是什么意思
- 玉麦面是什么意思
- 玉麦面果是什么意思
- 玉麦面糊是什么意思
- 玉麦须是什么意思
- 玉麦须须是什么意思
- 玉麦骨头是什么意思
- 玉麦;御麦;芋麦是什么意思
- 玉麦売売是什么意思
- 玉黄是什么意思
- 玉黄李是什么意思
- 玉黄李子是什么意思
- 玉黄膏是什么意思
- 玉黍是什么意思
- 玉黍黍是什么意思
- 玉黍黍花儿是什么意思
- 玉黍黍面是什么意思
- 玉鼎是什么意思
- 玉鼓筒是什么意思
- 玉鼓菜是什么意思
- 玉鼠是什么意思
- 玉鼻騂是什么意思
- 玉鼻骍是什么意思
- 玉齍是什么意思
- 玉齒是什么意思
- 玉齿是什么意思
- 玉龍是什么意思
- 玉龍形觿是什么意思
- 玉龍筆架是什么意思
- 玉龍紋玦是什么意思
- 玉龍紋觥是什么意思
- 玉龍膏是什么意思
- 玉龍虎併體帶鈎是什么意思
- 玉龍首鐲是什么意思
- 玉龙是什么意思
- 玉龙与怪鸟是什么意思
- 玉龙佩是什么意思
- 玉龙克尔河是什么意思
- 玉龙冰川是什么意思
- 玉龙喀什河是什么意思
- 玉龙夜战三更月,铁马秋行万里空。是什么意思
- 玉龙山是什么意思