柯布-道格拉斯生产函数

由两位美国经济学家查利斯·柯布(Charles W.Cobb)和保尔·道格拉斯(Paul Douglas)提出并因此得名的一种生产函数。代数形式为Y=AL2C1-2，这里Y表示国民产出，L是劳动的投入量，C是资本的投入量，A和α是大于零的常数(α<1)。这个生产函数是一阶线性齐次函数，经济含义为规模报酬稳定不变。如果每种生产要素按其边际产品获取报酬，工资在总产出中的相对份额是α，资本的报酬在总产出中的相对份额是1-α；或者说，劳动对总产出的贡献是资本对产出的贡献的α/1-α倍。这个生产函数是作为一种经验假定，于20世纪30年代提出来的，用来解释自1899年到1922年，美国的工资份额在国民收入中的相对稳定性。

柯布-道格拉斯生产函数CobDouglas Production function

经济学中使用最广泛的一种生产函数形式，它在数理经济学与经济计量学的研究与应用中都具有重要的地位。它是以美国数学家C.W.柯布和经济学家保罗.H.道格拉斯的名字命名的。柯布和道格拉斯根据美国制造业1899年到1922年的统计资料，发现指数型函数比其他数学函数更适合于描述生产过程。柯布-道格拉斯生产函数的一般形式可以表示为Q=AL^αK^β，其中，Q代表产量，L为劳动投入量，K代表资本投入量，A代表一定的技术水平，0<α<1,0<β<1。它描述了产出品与各投入品之间的一种实物关系。柯布-道格拉斯生产函数中，如果有任何一种投入品为零，则产出也为零，因此对于生产来说，每种生产要素都是必需的，没有一种要素可以完全替代另一种要素。如果每一种要素按其边际产品获得报酬，则函数中α和β分别代表劳动和资本在总产量中所占的相对份额，它们不随Y、L、K三个变量的改变而改变，在国民收入中所占的份额始终保持稳定。因此这一函数也被应用于分配理论中，为边际生产率分配论提供依据。柯布-生产函数还有一些有用的特性。(1)边际产量。

因此，边际产量只与要素投入的比例K/L有关，如果K、L投入量不变，或增加同样倍数，则边际产量不变。(2)产出弹性。

因此，α代表劳动的产出弹性，β代表资本的产出弹性。(3)规模报酬。将原投入量K、L扩大λ倍并代入生产函数得

该函数的规模报酬取决于α+β的值。当α+β>1是规模报酬递增；当α+β=1是规模报酬不变；当α+β<1是规模报酬递减。(4)替代弹性。

因此要素价格的相对变动将引起要素投入比例的相同变动。通过将函数两边取对数，可以将柯布-道格拉斯生产函数转化为较简单的线性函数，即

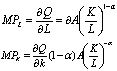
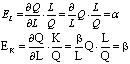
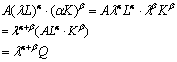
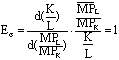
1nQ=1nA+α1nL+β1nK

这一形式被广泛地用于经济计量检验以及估计生产函数。运用最小二乘法，可以对其中的参数α、β、1nA进行估计。柯布-道格拉斯生产函数中技术进步是脱离了劳动与资本而单独存在的，这与实际生产过程不符； 另外实际生产中所使用的生产要素不只包括劳动和资本。但由于其具有很好的性质，因此仍然被广泛地应用。

柯布-道格拉斯生产函数CobbDouglas production function

柯布-道格拉斯生产函数是生产函数的一种特殊形式，其代数式为：Q=AL^αK^β。其中，A是常数，取决于投入与产出的度量单位，α和β则是表征劳动和资本在生产过程中相对重要性的常数，通常情况下α和β均大于0而小于1。柯布-道格拉斯生产函数有一个重要特性：当α+β=1时，该生产函数的规模收益不变；当α+β>1时，该生产函数的规模收益递增；当α+β<1时，该生产函数的规模收益递减。此外，在这一函数中，α、β恰好分别是劳动L、资本K的产出弹性。
柯布-道格拉斯生产函数应用广泛，但也存在两个重大缺陷。首先是它不允许存在这样一种有现实意义的生产可能性：在产量较低时规模收益递增；在产量达到中等水平时规模收益不变；在产量较高时规模收益递减。其次是它暗示着：当沿同一条等产量线移动时，边际技术替代率是不断变化的，这样，它就不能用来描述要素间的边际技术替代率接近常数的生产状况。
柯布-道格拉斯生产函数最早是由数学家柯布和经济学家道格拉斯于20世纪30年代提出来的，故而得名。