两平面垂直的性质定理

---

定理1 如果两个平面垂直，那么在一个平面内垂直它们交线的直线垂直另一个平面，用符号表示为

α⊥β，α∩β=a，，．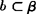

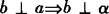定理2 如果两个平面互相垂直，那么经过第一个平面内的一点垂直于第二个平面的直线在第一个平面内，用符号表示为

α⊥β，P∈α，P∈a，．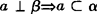

例 已知：α⊥γ，β⊥γ，α∩β=l，

求证：l⊥γ．

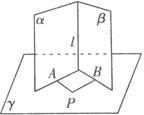
证法一 在γ内取一点P，作PA垂直于α与γ的交线于A，PB垂直于β与γ的交线于B，则PA⊥α，PB⊥β，∵l=α∩β，∴l⊥PA，l⊥PB，∵α与β相交，∴PA与PB相交，又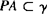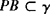，，∴l⊥γ．

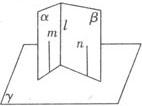
证法二 在α内作直线m垂直于α与γ的交线，在β内作直线n垂直于β与γ的交线，∵α⊥γ，β⊥γ，∴m⊥γ，n⊥γ，∴m∥n，又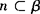，∴m∥β，∴m∥l，．l⊥γ．

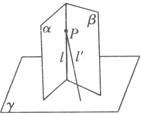
证法三 在l上取一点P，过P作γ的垂线l′．

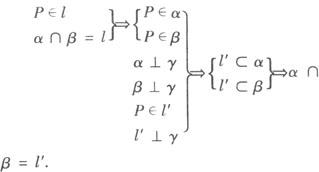
但α∩β=l∴l与l′重合，∴l⊥γ．

点评 证法一、证法二都是利用“两平面垂直时，在一个平面内垂直于两平面的交线的直线垂直于另一个平面”的这一性质，添加了在一个平面内垂直于交线的直线这样的辅助线，这是证法一、证法二的关键．

证法三是利用“如果两个平面互相垂直，那么经过第一个平面内的一点垂直于第二个平面的直线，在第一个平面内”这一性质，添加了l′这条辅助线，这是证法三的关键．

通过比较，应仔细体会两平面垂直时，添加辅助线的方法．