三角和方法

---

近代解析数论的重要方法。

它是由苏联数学家维诺格拉陀夫所首创，我国数学家华罗庚对该方法的发展作了重要贡献。维氏用三角和方法与圆法相结合首先证明了奇数的哥德巴赫猜想(即每个不小于9的奇数都是三个奇素数之和)是成立的。所谓“三角和”或“指数和”就是形如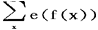(x))的和，其中e(f(x)=e^2πi^f(x)(=cos(2πf(x))+isin(2πf(x))，f(x)是实函数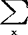，表示对某一指定的x的整数集合求和。例如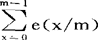，就是一种最简单的三角和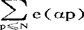；也是一种重要的三角和，其中α为实数，p为素数。著名的关于奇数的哥德巴赫猜想的证明就要用到这种三角和的一个上界估计。在数论里，有许多著名问题都和三角和有著极其密切的关系。一个重要问题的解决常常依赖于一种三角和的估计。因此，各种类型的三角和的估计，常常变成数论的中心问题和关键所在，这是因为某些三角和有著许多特殊的性质，正是由于这些性质，才使得许多困难的数论问题可以转化为三角和的问题。一些重要的三角和的性质有：(1)设m是正整数，a是整数，则那m｜a时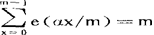，，当m／a时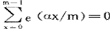，；(2)设m是正整数，p为素数，(p，m)=1，L≥1为正整数，则当L=1时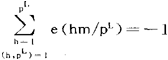，，当L＞1时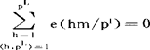；(3)设q，m为正整数，(m，q)=1，则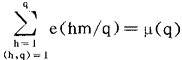，其中μ(q)为茂陛乌斯函数，利用性质(1)，就可以将同余方程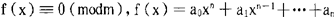(其中a₀，a₁，…a_n是整数)的解答个数表为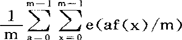，对于多变量的整系数同余方程或同余方程组的解答数也有类似的形式。经此表达后，同余方程的问题便得到了解析形式，从而可用解析方法对它进行研究。

与性质(1)相当的公式是：当n=0时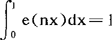，，n≠0时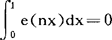，。由此立即可以推得丢番图方程f(x₁，x₂，…，xn)=N，ai≤xi≤bi，(i=1，2，…n)的整数解的组数等于。

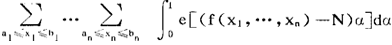例如，著名的费马大定理(即xⁿ+yⁿ=zⁿ，当n≥3时，无非零整数解)就在于证明：当n≥3时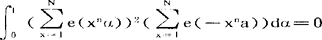，；哥德巴赫问题则在于证明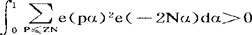。在数论里，还有许多重要问题的研究与解决都要用到三角和。象华林问题，圆内格点问题以及除数问题等等。