多面体截面的画法duomianti jiemian de huafa

主要根据是：
❶确定平面的条件；
❷若两个不重合的平面有一个公共点，则它们相交于过这点的一条直线；
❸若一条直线上的两点在一个平面内，则这条直线上所有的点都在这个平面内；
❹若一条直线平行于一个平面，经过这条直线的平面和这个平面相交，则这条直线就和交线平行.
画多面体的截面的关键是确定截点，当位于多面体同一平面上的两个截点确定之后即可连接成截线，从而作出截面.

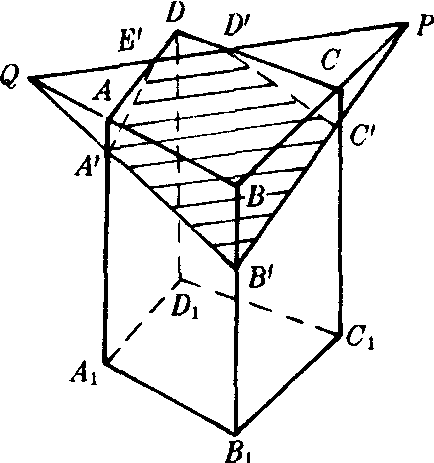
例 如图，ABCD-A₁B₁C₁D₁是一个四棱柱，A′,B′,C′分别是侧棱AA₁,BB₁,CC₁上的点，求作过A′,B′,C′三点的截面.
解 连结B′C′与BC 的延长线交于P.因为B′C′⊂平面A′B′C′，所以P∈平面A′B′C′.
连结B′A′与BA的延长线交于Q.因为B′A′⊂平面A′B′C′，所以Q∈平面A′B^′C′.
因为P∈BC,Q∈BA，所以P∈平面AC,Q∈平面AC.
连结PQ，直线PQ和CD,AD分别交于D′,E′.
连结A′E′,C′D′, D′E′，则A′E′⊂平面A₁D,C′D′⊂平面C₁D,D′E′⊂平面AC.
因此五边形A′B′C′D′E′就是所求的截面.