分布型指数法methods of distributionpattern index

依据对某一种群抽样调查中所得的3个重要分布信息(均数、方差和样本数)之间的关系，判别此种群个体间的扩散或聚集程度，从而确定其分布型的一种方法。常用的分布型指数有扩散系数、k值法、扩散型指数、泰勒指数、平均拥挤度和ρ指数等6类。
扩散系数(C) 是方差与均数的比值，用以检验种群扩散是否属于随机型的一个系数。其公式为：

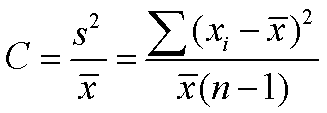
式中为平均虫数； S²为方差； n为抽样数。若种群的扩散完全是随机的，则C应是符合均数为1，方差为2n/(n-1)²的正态分布。应用时，应统计出C=1的概率为95%的置信区间为：

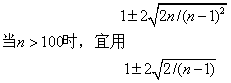
式中 n为抽样数。如实际估算的C值落入上式范围内，则为随机分布； C大于此范围时，为聚集分布。先调查统计种群密度不同的若干田块，检验C与种群密度的关系。如发现C与种群密度相关，则不宜用此法。
扩散系数也可用X²检验是否呈随机分布型：

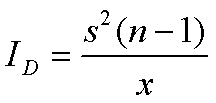
ID的分布与自由度为(n-1)的X²分布相似。故若计算所得ID≤X²_0.05时，为随机分布； ID>x0.052时，则为聚集分布。
k值法 这一类包括k值、C_A指数、种群群集均数(λ)3种，用以估计种群的聚集度。❶k值即负二项分布概率通式中的参数k:

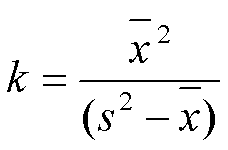
k值愈小，表示聚集程度愈大； 如k→∞，则分布趋于泊松分布。k值与种群密度无关，但与取样单位大小有关，故只能对相同大小的取样单位进行比较。
❷C_A数是k值的倒数，可作为k值的补充：

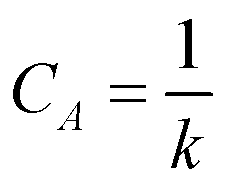
若C_A＝0，为随机分布（泊松分布）; C_A>0为聚集分布； C_A<0为均匀分布。
❸种群群集均数(λ)是另一种k值法。种群的聚集可由其本身群集行为引起，也可由环境条件(如微气候、土壤、植物生长发育状况或天敌等)不匀均性造成。群集均数(λ)可用以分析聚集的起因。

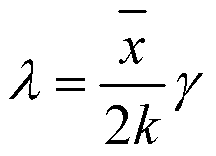
式中 r为分布表中自由度等于2k、 概率为0.5时应处的x2值。当λ<2时，聚集可能是某些环境条件差异所引起； 当λ≥2时，则可能由昆虫本身行为或外界因素之一所引起。
扩散型指数(Iσ) 森下正明1959年提出。其最大优点是分布型与抽样数、抽样单位大小均无关。其公式为：

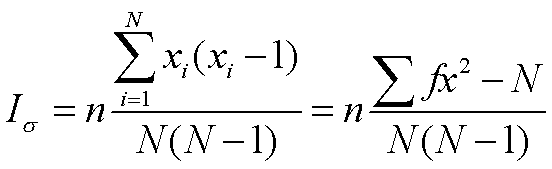
式中 n为抽样数； N为总虫数；X_i为第i个样本中的虫数；f为样本数。当Iσ为1时，属随机分布；Iσ>1时，属聚集分布； Iσ<1时，属均匀分布。
泰勒指数(b) 泰勒(L. R. Taylor,) 1961年提出，表示生境对物种聚集的作用。不少动物取样中，均数(m)与方差(s²)之间呈幂函数关系：

s²＝am^b

经对数代换后，可呈直线回归：

1gs²＝1ga+b1gm

式中 a表示抽样因素，b则为聚集特征指数。当b→0，趋向于均匀分布；b=1，为随机分布；b→∝，则高度聚集。
平均拥挤度() 这一类包括平均拥挤度和聚集指数两种。
平均拥挤度(mean crowding,) 劳埃德(M·Lloyd)1967年提出，又称劳埃德平均拥挤度。表示“每个样方中对于每个个体来说挤在一起的平均邻居数”的参数。以为信息的各种指数，受零样方影响，难以反映种群密度的实况，而强调个体的平均，不受零样方的影响。其公式为：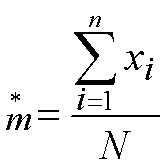

0	2	0	0	1
3	0	2	0	1
0	0	1	3	0
1	4	0	0	2

式中 x_i为第i样方内每个个体的邻居数；N为总个体数。例如下图示20个个体分布于20个样方内，从第一列左起，依次写出各样方内的邻居数(xi):1,1;0;2,2,2; 1,1; 0; 0;2,2,2;0;3,3,3,3;1,1。∑x_i＝30,N=20，代入上式：

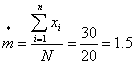
平均拥挤度()与平均密度()及方差(s²)的关系为：

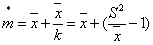
式中 k为负二项分布型的参数。当k→∝,＝，种群呈泊松分布。k很小，>时，呈聚集分布。为计算更精确，可采用下式：

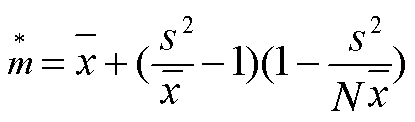
聚集指数(/) 日本岩俊一(Iwao)1971年提出。当/等于1时为泊松分布，大于1时为聚集分布，小于1时为均匀分布。并提出以对的直线回归方程检验分布型：

＝α+β

式中 α说明分布的基本成分，α=0时为单个个体，α>0时为个体群，α<0时个体互斥。β说明基本成分的空间分布型，β=1时，为随机分布；β>1时，为聚集分布；β<1时，为均匀分布。根据α和β的不同组合，亦可分析种群的分布型；当α=0,β=1，呈随机分布；α<0,β>1，呈均匀分布；当❶α>0,β=1；或
❷α=0,β>1；或
❸α>0,β>1时，种群呈聚集分布。其中，❶式组合呈奈曼A型分布，泊松一正二项分布；
❷式组合为具公共k值的负二项分布；
❸式组合呈普通负二项分布。
ρ指数表达了样方单位的大小从i—1增加到i时，的增量对增量的比值。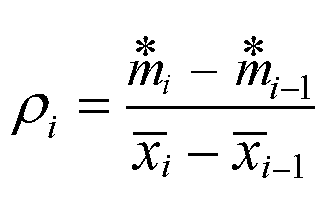

式中 i=1,2,3，………，代表样方由小到大时的顺序号，对最小的样方(i=1)，则ρ=/，即相当于上述聚集指数。ρ指数除可用以分析种群空间分布型外，特别可用于估计个体群的面积。以样方单位的大小为横坐标，ρi值为纵坐标作图，根据图形的变化测定个体群的面积。❶当分布的基本成分为个体或为密集的个体群时，ρ<1，样方小于个体群面积； ρ≥1，样方大于个体群面积；
❷当分布的基本成分为疏松的个体群时，ρ>1，样方小于个体群面积；ρ值显著下降，样方大于个体群面积。在二者的转折点处（如图上的箭头），所对应的样方单位大小，即可表示个体群的面积（见图）。

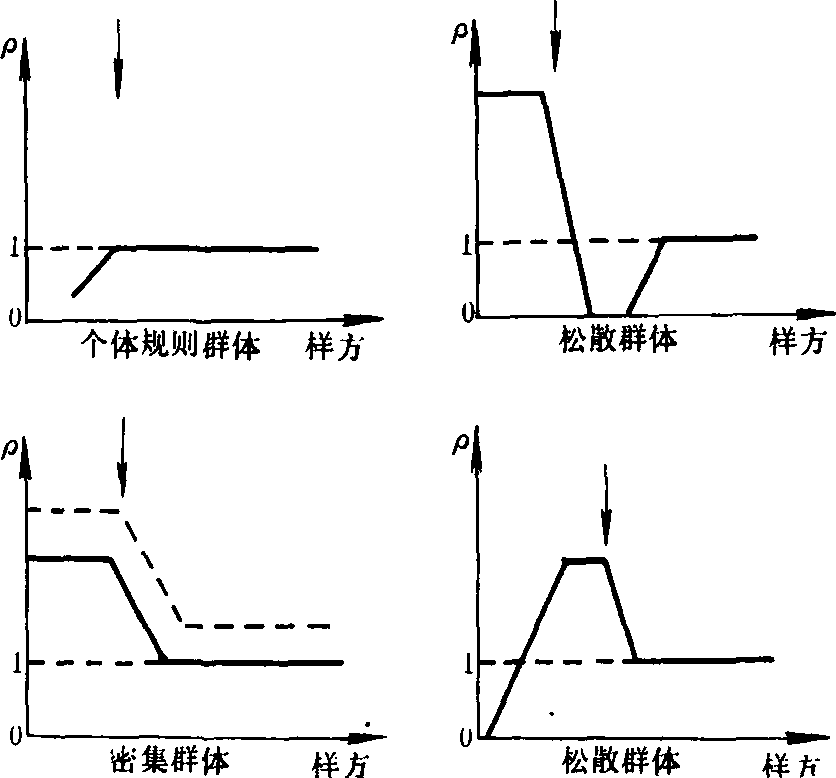
样方大小和ρ值关系图

(据T.R.E. Southwood)