代数法解作图题daishufa jie zuotuti

用代数手段求出某线段以解作图题的方法.解作图题时，往往归结为求出某一线段，而此线段又常借助于代数法求出.
例如，已知梯形，求作底的平行线使其平分该梯形的面积.

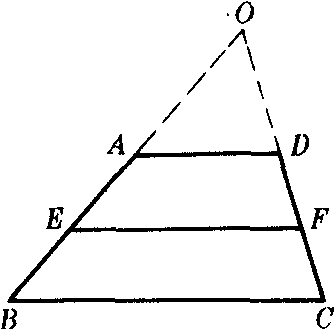
已知 梯形ABCD,AD∥BC.
求作 直线EF∥BC，使其平分梯形面积.
分析 如图，延长BA,CD交于O，则△OBC∽△OEF∽△OAD.设OB=

a, OA=b, OE=x,

那么，

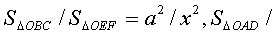
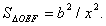
因此，

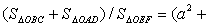
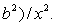
但是

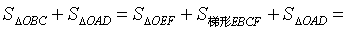
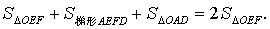
所以

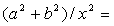
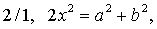
因此，

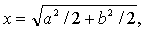
设y=

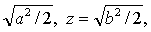
则

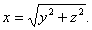
作法
❶作a,a/2的比例中项，得y；求b,b/2的比例中项得z;
❷以y,z为直角边作直角三角形.设斜边的长为x;
❸在OB上取OE=x₁，作EF∥BC.则EF就是所求的直线.
用代数法解作图题的步骤是：
❶用字母表示已知线段和求作的线段；
❷按问题中已知关系和已知的定理列出方程（或方程组）;
❸解这个方程（或方程组），以代数式表示它的根，即用已知线段表示求作线段的代数式；
❹根据此代数式逐步作图，直到作出所求作的图形.