不定积分
不定积分budingjifen
设F (x)是函数f (x)的一个原函数,则函数f (x) 的全体原函数F (x) +C(C是任意常数) 称为f (x) 的不定积分,记作
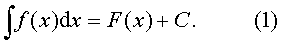
由不定积分的定义可知,∫f(x)dx表示一个含有无穷多个原函数的函数族,即 {F (x)+C|-∞
不定积分有以下基本性质:
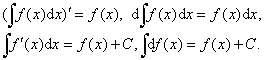
☚ 原函数 不定积分的几何意义 ☛
不定积分
见“原函数”。
不定积分
indefinite integral
- 脑血栓形成是什么意思
- 脑血栓形成是什么意思
- 脑血栓形成的药物治疗是什么意思
- 脑血液供应是什么意思
- 脑血管、神经系统疾病的眼部表现是什么意思
- 脑血管性痴呆是什么意思
- 脑血管意外是什么意思
- 脑血管疾病是什么意思
- 脑血管疾病是什么意思
- 脑血管病是什么意思
- 脑血管病所致精神障碍是什么意思
- 脑血管痉挛是什么意思
- 脑血管造影是什么意思
- 脑转移瘤的放疗是什么意思
- 脑转移癌是什么意思
- 脑部病变是什么意思
- 脑部肿瘤是什么意思
- 脑震伤片是什么意思
- 脑震荡是什么意思
- 脑震荡是什么意思
- 脑震荡及脑挫伤是什么意思
- 脑震荡后遗症是什么意思
- 脓性指头炎是什么意思
- 脓性指头炎是什么意思
- 脓毒败血症性流产或脓毒败血症性休克是什么意思
- 脓气胸是什么意思
- 脓疱性银屑病是什么意思
- 脓疱疮是什么意思
- 脓疱疮是什么意思
- 脓疱疮是什么意思
- 脓疱症是什么意思
- 脓癣是什么意思
- 脓皮病是什么意思
- 脓肿是什么意思
- 脓肿性穿掘性头部毛囊周围炎是什么意思
- 脓胸是什么意思
- 脓胸是什么意思
- 脓胸是什么意思
- 脚手架产生事故的原因分析是什么意思
- 脚手架安全技术措施是什么意思
- 脚手架安全管理是什么意思
- 脚手架的作用是什么意思
- 脚手架的作用与要求是什么意思
- 脚手架的分类是什么意思
- 脚手架的要求是什么意思
- 脚气是什么意思
- 脚踏开关是什么意思
- 脚铃舞是什么意思
- 脱位是什么意思
- 脱位整复与固定是什么意思
- 脱位的发生与临床表现是什么意思
- 脱卤设备是什么意思
- 脱发是什么意思
- 脱口秀——广播电视谈话节目的威力与影响是什么意思
- 脱墨迹灵是什么意思
- 脱屑性红皮病是什么意思
- 脱敏疗法是什么意思
- 脱木质素的阶段性是什么意思
- 脱模润滑剂是什么意思
- 脱模阻力的计算是什么意思