ARIMA模型auto regressive integrating moving averagemodel

亦译“综合自回归移动平均模型”。考虑了时间序列的自回归特性和偏自回归特性，将自回归和移动平均分析技术结合起来的综合分析技术。是一种比较成熟的单变量平稳时间序列分析预测方法。
在AR模型和MA模型中，所考察的随机过程本身要求是平稳的，否则，通过差分使过程达到平稳后进行相应的分析。而ARIMA模型就是把差分、AR模型和MA模型结合在一起的模型，实际上是更为一般的表达式，用ARIMA(p,d,q)表示，其中的d是表示原过程本身达到平衡所需的差分次数。如果原过程用Xt表示，经d阶差分后获得平稳过程W_t,即W_t＝△^dXt，则称Xt为d阶齐次非平稳过程。完整的ARIMA(p,d,q)模型表示为：

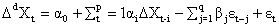
ARIMA(p,d,q)模型的参数估计一般是先确定原过程的平稳性，经d次差分获得平稳序列Wt后，使用W_t的自相关函数和偏自相关函数确定AR过程和MA过程的阶数(p,q)，然后估计模型的参数并进行相应的检验，确定模型的有效性，最后才可用于对原过程未来值的预测。

ARIMA模型ARIMA Model

现实中，我们处理的许多经济时间序列是非平稳的。但幸运的是，我们对可通过差分一次或更多次而将之转换为平稳的时间序列。然后，对转换后平稳的新序列建立ARMA模型。则对转换前非平稳的原序列而言，该模型为ARIMA模型。如果w_t＝△^dy_t是平稳序列，我们就称y_t是d阶可平稳化的非平稳过程。这里△表示差分，即：

△y_t＝y_t-y_t-1,△²y_t＝△y_t-△y_t-1

等等。我们可对w_t建立ARMA过程的模型。如果w_t是一个ARMA(p,q)过程，则我们称y_t是(p,d,q)阶可整的自回归-移动平均过程ARIMA(p,d,q):

φ(B)△^dy_t＝δ+θ(B)ε_t (1)

其中φ(B)=1-φ₁B-φ₂B²-…-φ_pB^p和θ(B)=1-θ₁B-θ₂B²-…-θ_qB^q。
我们称φ(B)为自回归算子和θ(B)为移动平均算子。
有可能平稳序列w_t不是混合的，即或是自回归或是移动平均。如果w_t是AR(p)，我们称y_t为(p,d)阶可整的自回归过程并记之为ARI(p,d,0)。如果w_t是MA(q)，我们称y_t为(d,q) 阶可整的移动平均过程并记之为IMA(0,d,q)。
如何选择最合适的p,d和q的值，即ARIMA模型的识别。可通过检查序列的自相关函数和偏自相关函数而得到部分解决。
给定序列y_t，对之建模的首要问题是确定可平稳化的差分次数d。我们可应用平稳序列的自相关函数ρ_k随着k增大而下降为0的结果来确定d。这是因为，对于(p,q)阶ARMA平稳过程，我们知道该过程的移动平均部分的自相关函数当k>q时为0，即这部分只有q期记忆力。我们也知道平稳ARMA过程自回归部分的自相关函数以几何级数下降为0。平稳ARMA过程的自相关函数前q-期有移动平均的特征。之后就反映出自回归的特征，以几何级数下降为0。为了确定d，首先检查原序列y_t的自相关函数，确定y_t是否平稳。如果y_t不平稳，再对差分后序列△y_t的自相关函数进行检查。重复这个步骤直到有某个d使得w_t＝△^dy_t是平稳的。即自相关函数当k增大时趋向于0。也应该检查时间序列本身，如果它有某种趋势，则必不平稳，就必须对它进行差分。d确定后，计算平稳序列w_t＝△^dy_t的自相关函数和偏自相关函数以确定p和q。对于低阶过程的识别较容易，因为 参 照 Robert S.Pindyck & Daniel L.Rubinfeld“Econometric Models and Economic Forecasts”(Fourth Edition)图17.1到图17.10很容易对AR(1),AR(2),MA(1),MA(2)和ARMA(1,1)进行识别。然而，如果序列不是低阶的ARMA过程，则高阶p和q的确定将比较困难，这需要对自相关函数，偏自相关函数仔细的审查。例如自相关函数有钉形形状表明有移动平均项，偏自相关函数可用于确定过程自回归部分的阶数。
如果过程的自回归和移动平均部分都是高阶的，我们能做的仅仅是对p和q进行猜测。在ARMA(p,q)模型的参数被估计之后，就可对猜测进行检验。诊断检验的第1步是计算已估ARMA(p,q)模型的残差项的自相关函数，第2步是确定残差是否为白噪声。如果不是白噪声，必须尝试新的识别。