定积分的近似计算

---

矩形法 矩形法是把曲边梯形分成若干个窄曲边梯形，然后用窄矩形的面积来近似代替窄曲边梯形的面积，从而求得定积分的近似值的方法．

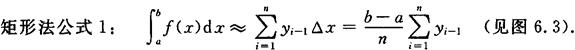
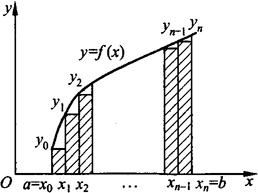
图6．3

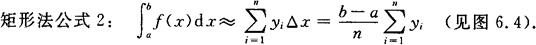
图6．4

梯形法 梯形法是把曲边梯形分成若干个窄曲边梯形，然后用窄梯形的面积来近似代替窄曲边梯形的面积，从而求得定积分的近似值的方法．

梯形法公式：

图6．5

抛物线法 抛物线法是将曲线分为许多小段，用对称轴平行于y轴的二次抛物线上的一段弧来近似代替原来的曲线弧，从而得到定积分的近似值的方法．

用分点a=x₀，x₁，…，x_n=b把区间分成n(偶数)等分，这些分点对应曲线上的点为M_i(x_i，y_i)(y_i=f(x_i))(i=0，1，2，…，n)(见图6．6)．

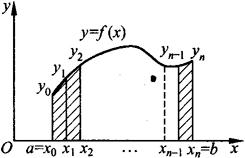
图6．6

抛物线法公式(辛普森(Simpson)公式)：

无穷限的广义积分定义 设函数f(x)在区间［a，+∞)上连续，取b＞a，如果极限

存在，则称此极限为函数f(x)在无穷区间［a，+∞)上的广义积分，记作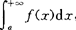，即

当极限存在时，称广义积分收敛；否则，称广义积分发散．

类似地，设函数f(x)在区间(－∞，b］上连续，取a＜b，如果极限

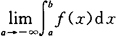
存在，则称此极限为函数f(x)在无穷区间(－∞，b］上的广义积分，记作，即

设函数f(x)在区间(－∞，+∞)上连续．如果广义积分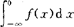和都收敛，则称上述两广义积分之和为函数f(x)在无穷区间(－∞，+∞)上的广义积分，记作，即

极限存在称广义积分收敛；否则称广义积分发散．

例如，广义积分，当p＞1时收敛，其值为；当p≤1时发散．

无界函数的广义积分定义 设函数f(x)在区间(a，b］上连续，而在点a的右邻域内无界．取ε＞0，如果极限

存在，则称此极限为函数f(x)在区间(a，b］上的广义积分，记作，即

当极限存在时，称广义积分收敛；否则，称广义积分发散．

类似地，设函数f(x)在区间［a，b)上连续，而在点b的左邻域内无界．取ε＞0，如果极限

存在，则称此极限为函数f(x)在区间［a，b)上的广义积分，记作，即

当极限存在时，称广义积分收敛，否则，称广义积分发散．

设函数f(x)在区间［a，b］上除点c(a＜c＜b)外连续，而在点c的邻域内无界．如果两个广义积分

都收敛，则定义

否则，就称广义积分发散(定义中c为瑕点，以上积分也称为瑕积分)．