例1 已知抛物线y2=—8x,过点P0(—1,1)引一条弦,使此弦在P0点被平分,求弦所在的直线方程.
解 设所求弦的直线方程为
y—1=k(x+1),
即y=kx+k+1
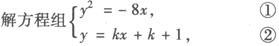
把❶ 代入❷ 得
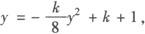
即ky2+8y—8k—8=0.
设所求弦的两端点为(x1,y1),(x2,y2)由韦达定理,得
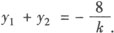
又∵P0(—1,1)是弦的中点,
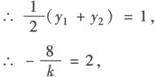
即k=—4.
∴此弦所在直线方程为:
4x+y+3=0,
例2 A、B是抛物线y2=2px(p>0)上的两点,且OA⊥OB(O为坐标原点),求证:
(1)A、B两点的横坐标之积,纵坐标之积分别都是定值;
(2)直线AB经过一个定点.
证明 (1)设A(x1,y1),B(x2,y2),则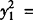
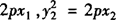 .
.
因为OA⊥OB,所以x1x2+y1y2=0,
所以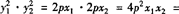 —4p2y1y2,
—4p2y1y2,
所以y1y2=—4p2为定值,x1x2=—y1y2=4p2也为定值.
(2)因为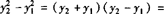 2p(x2—x1),
2p(x2—x1),
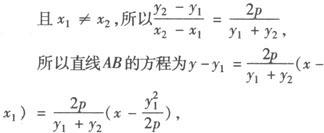
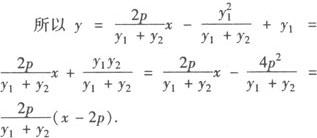
所以直线AB过定点(2p,0).
例3 抛物线C的顶点在原点,焦点在x轴正半轴上,若点A(—1,0)和点B(0,8)关于过圆点O的直线l的对称点都在C上,求直线l和抛物线C的方程.
策略 本题可用待定系数法,设出直线l和抛物线C的方程,再求出点A和B关于l的对称点A′和B′,根据A′、B′的坐标(含参数)满足抛物线方程得出关于两个参数的方程组,解出参数值即可求出l和C的方程.
解 由题意设直线l和抛物线C的方程分别为y=kx(k≠0)和y2=2px(p>0).
设A(—1,0)和B(0,8)关于l的对称点分别为A′(x1,y1),B′(x2,y2),

∵A′、B′在抛物线C上.
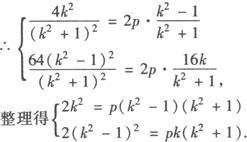
❶ ÷❷ 消去p,整理得k=k2—1,
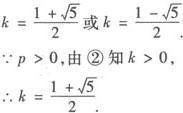
把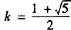 代入❶ 得
代入❶ 得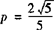 .
.
所以,直线l的方程为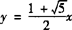 ,抛物线C的方程为
,抛物线C的方程为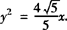 .
.
- 端木生涯是什么意思
- 端木皓珍是什么意思
- 端木绰是什么意思
- 端木缙是什么意思
- 端木蕻良是什么意思
- 端木蕻良《有人问起我的家》是什么意思
- 端木蕻良《有人问起我的家》赏析是什么意思
- 端木蕻良《黎明的眼睛》是什么意思
- 端木蕻良《黎明的眼睛》赏析是什么意思
- 端木虹是什么意思
- 端木赐是什么意思
- 端木辞金是什么意思
- 端木采是什么意思
- 端木野是什么意思
- 端木露西是什么意思
- 端木鸟是什么意思
- 端木鹤田是什么意思
- 端末调理员是什么意思
- 端本是什么意思
- 端本堂是什么意思
- 端本正源是什么意思
- 端本清源是什么意思
- 端本澄源是什么意思
- 端本肇末是什么意思
- 端杂绪棼是什么意思
- 端板是什么意思
- 端极是什么意思
- 端林是什么意思
- 端枪是什么意思
- 端架是什么意思
- 端架儿是什么意思
- 端架子是什么意思
- 端树虫是什么意思
- 端框架是什么意思
- 端棍是什么意思
- 端楷是什么意思
- 端正是什么意思
- 端正严肃是什么意思
- 端正书写姿势的技能是什么意思
- 端正党风、惩腐倡廉必须加强监督是什么意思
- 端正党风的有效措施是什么意思
- 端正其行为是什么意思
- 端正凝重是什么意思
- 端正刚强是什么意思
- 端正合适是什么意思
- 端正地坐着是什么意思
- 端正地坐着静静地思考问题是什么意思
- 端正地站着是什么意思
- 端正均称是什么意思
- 端正外形是什么意思
- 端正好是什么意思
- 端正好·上高监司是什么意思
- 端正好(正宫)是什么意思
- 端正容态是什么意思
- 端正容颜是什么意思
- 端正庄重是什么意思
- 端正德行是什么意思
- 端正志向是什么意思
- 端正思想是什么意思
- 端正恭谨是什么意思