直线与平面平行的性质定理

---

如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和交线平行，用符号表示为

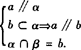
例1 A、B、C、D四点不共面，M、N分别是△ABD、△BCD的重心，求证：MN∥平面ACD．

证明 连结BM、BN并延长分别交AD、DC于P、Q两点，连PQ．

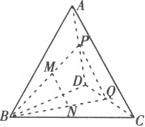
M、N分别是△ABD、△BCD的重心

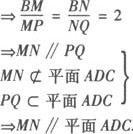
点评 研究图形还可得出如下结论：

MN∥PQ∥AC，AC∥平面BPQ．

例2 已知：如图，α∩β=l，a∥α，a∥β

求证：a∥l．

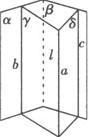
策略 用“线线平行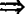线面平行”．

证明 过a作平面γ交平面α于b

∵a∥α，∴a∥b；

同样，过a作平面δ交平面β于c．

∵a∥β，∴a∥c；

．．b∥c．

又∵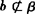且，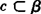

∴b∥β．

又平面α经过b交β于l，

∴b∥l，且a∥b．

∴a∥l．

点评 证明与平行有关的问题时，线面平行的判定定理，性质定理，三线平行公理常结合起来使用，并常用下面的关系：

本题也可用反证法、同一法，请读者自己探讨．