用系统开环频率特性分析系统稳定性

---

(1)奈奎斯特稳定判据

奈奎斯特稳定判据的特点是用系统的开环幅相频率特性来判别闭环系统的稳定性。该判据为：一个反馈系统其闭环传递函数在右半s平面的极点数Z，可以根据其开环传递函数在右半s平面的极点数P和当ω由零变到无穷大时的开环幅相频率特性曲线包围(－1，j0)点的圈数N(沿ω增加方向，逆时针包围为正)来决定，即

Z=P－2N(5．5－2)

Z等于零，则闭环系统稳定；Z不等于零，闭环系统不稳定。Z的值就是闭环传递函数在右半s平面极点的个数。

例1若反馈系统开环传递函数为

(2)系统开环传递函数中含有积分环节时奈氏判据的应用

当系统开环传递函数含有积分环节时，就意味著开环传递函数有在原点的极点，这时在应用奈氏稳定判据时应做如下处理：

(A)把开环传递函数在原点的极点视为s平面左半平面的极点；

(B)因为把开环传递函数在原点的极点视为左极点，则需对开环奈氏图做出补充，以图5．5－7(a)、(b)分别为系统开环传递函数有一个和两个积分环节的情况做例子，它们的奈氏曲线需从ω=0⁺开始，以R→。。为半径，沿逆时针方向补画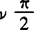角度的圆弧(v为开环传递函数中积分环节的个数)，如图5．5－7(a)、(b)中的虚线部分，虚线圆弧在ω=0处与实轴相交。

当做完上述处理后，再应用奈氏判据判别系统稳定性。

对图5．5－7(a)对应的系统，若P=0，从图中看出，其奈氏曲线包围(－1，j0)点的圈数N=－1，这样Z=0－2×(－1)=2，故其闭环系统不稳定；对图5．5－7(b)对应的系统，若P=0，其奈氏曲线包围(－1，j0)点的圈数N=0，Z=0－2×0=0，故其闭环系统是稳定的。

(3)对数频率特性的稳定性判据

A．穿越

在L(ω)＞0的频率区间，φ(ω)曲线通过－π线称为穿越。沿ω增加方向，φ(ω)曲线自下向上通过－π线(φ角增加)为正穿越，反之，φ(ω)曲线自上向下通过－π线(φ角减小)为负穿越。

B．对数频率特性的稳定性判据

一个反馈系统，其闭环传递函数在右半s平面的极点数Z，可以根据开环传递函数在右半s平面的极点数和开环对数幅频特性为正值的所有频率范围内，对数相频特性的正、负穿越数之差N来确定，即

Z=P－2N

当Z等于零时，闭环系统是稳定的。

例2 若一个反馈系统的开环传递函数为