欧拉方程

---

是解变分问题的一个基本工具，它给出泛函极值存在的一阶必要条件。

设J(y)是定义于某集D上的一个泛函，D含于某个函数空间y。对给定y∈D，若对任何h∈y，导数：

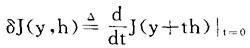
存在，则说泛函J在y处存在变分，且称映射

h→δJ(y，h)

为J在y的变分，记作δJ(y)。

若J(y)在某点y^*∈D取得极值且变分存在，则必定δJ(y^*)=0，即y=y^*满足方程：

δJ(y)=0 (*)

方程(*)就是关于J的欧拉方程。因此，求泛函J(y)的极值点归于解欧拉方程(*)，这正是欧拉方程意义之所在。

在很多具体问题中，泛函J(y)通常表为某个积分，而欧拉方程则可转化为一个微分方程。例如，设

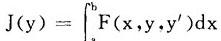
其中F是已知的二次可微函数，则相应的欧拉方程可化为

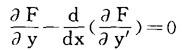
这是一个关于未知函数y的二阶常微分方程。