期望效用函数

---

用以表达在不确定情况下的偏好关系。

在消费者理论中，消费者在他的预算限制下选择一个使其效用最大的物品向量。有时消费者要选择的不是一个确定的物品向量，而是一个不确定的前景。这一不确定的前景可比作一张彩券。一般地，一张彩券可记为p°x+(1－p)°y，即以概率p获得物品向量x，以(1－p)的概率获得物品向量y，记所有彩券的集合为L。

设消费者的偏好关系满足如下3个性质：

❶ 完全性。对L中任何两张彩券A、B，或者A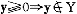B，或者B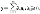A，或者A～B。

❷ 返身性。对所有A∈L，有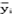AA。

❸ 传递性。

对L中任何3张彩券A、B、C，如果A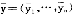B，B#C，则A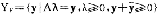C。

于是，如果在L上存在一个函数u(·)，满足

p°x+(1－p)°y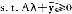q°w+(1－q)°z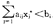u(p°x+(1－p)°y)≥u(q°w+(1－q)°z)及

u(p°x+(1－p)°y)=pu(x)+(1－p)u(y)，则称u(·)为关系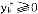的期望效用函数。可以证明，在很一般的条件下，期望效用函数是存在的。