最小二乘法

---

亦称“最小平方法”。使对因变量的估计值与实际观测值之差的平方达到最小。目前常见的回归分析方法之一，是进行回归分析的基础。又被称作“ordinary least quare”(可译为“普通最小二乘法”或“普通最小平方法”)。这一方法最早由勒让德提出，后经G．F．Guass和P．S．Laplace引入统计学研究之中。下面用一个线性回归模型来具体说明这一方法。

对于回归模型：

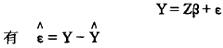
式中，Y是被解释变量向量；Z是解释变量向量；u是白噪声向量；其均值为零，方差为σ²；β是待估参数。最小二乘法要求待估的回归方程使得的平方和达到最小，即：

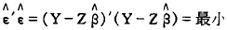
因为Y和Z是已知的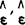，的大小完全取决于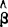的大小，而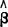是由估计方法确定的参数。因此，根据微积分中求极值的原理，当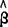的一阶导数等于零时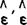，才能达到最小值，因而有：

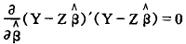
整理后有常规方程：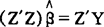

如果(Z’Z)^－1存在，以上常规方程有解：

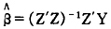
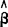就是回归模型Y=Zβ+ε的普通最小二乘估计值，它使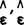达到最小。

由于现实生活中往往出现违背线性回归模型的基本假设，如异方差性、多重共线性、残差自相关等等，以致矩阵(ZZ)近于退化，很难用普通最小二乘法进行模型参数估计。为此出现了基于它的一些更为一般和适用的方法，如广义最小二乘法、加权最小二乘法、间接最小二乘法、工具变量法、约束最小二乘法等等。