(1)D(aξ+b)=a2Dξ;(2)Dξ=Eξ2—(Eξ)2.
例1 已知随机变量ξ的期望Eξ=4,方差Dξ=1,则η=2ξ—5的期望Eη=__,方差Dη=____.
解 直接利用期望和方差的性质即可.
∵E(aξ—b)=aEξ—b,
..Eη=E(2ξ—5)=2Eξ—5=2×4—5=3,又∵D(aξ+b)=a2Dξ,
∴Dη=D(2ξ—5)=4Dξ=4×1=4.
例2 设某运动员投篮投中的概率为P=0.6.(1)求一次投篮时投中次数ξ的期望和方差;
(2)求重复5次投篮投中次数η的期望和方差.
解 (1)投篮一次可能投中,或可能不中,投中次数ξ服从两点分布;(2)重复5次投篮的投中次数ξ服从二项分布.
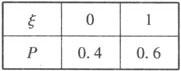
(1)ξ的分布列为:
由期望的定义可得:
Eξ=0×0.4+1×0.6=0.6.
由方差的定义可得:
Dξ=(0—0.6)2×0.4+(1—0.6)2×0.6=0.36×0.4+0.16×0.6=0.144+0.096=0.24.
(2)根据题意知η~B(5,0.6).
η的分布列为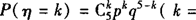 0,1,2,3,4,5),即
0,1,2,3,4,5),即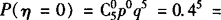 0.01024,
0.01024,
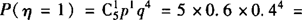 0.0768,
0.0768,
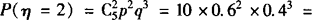 0.2304,
0.2304,
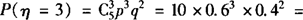 0.3456,
0.3456,
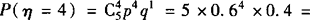 0.2592,
0.2592,
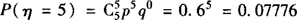 ,
,
Eη=0×0.01024+1×00768+2×0.2304+3×0.3456+4×0.2592+5×0.7776=3,
Dn=(0—3)2×0.01024+(1—3)2×0.0768+(2—3)2×0.2304+(3—3)2×0.3456+(4—3)2×0.2592+(5—3)2×0.0776=1.2.
例3 求证:Dξ=Eξ2—(Eξ)2.
证明 Dξ=(x1—Eξ)2P1+(x2—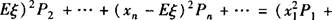
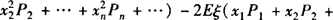 …+xnPn+…)+(Eξ)2(P1+P2+…+Pn+…)=Eξ2—2(Eξ)2+(Eξ)2=Eξ2—(Eξ)2.
…+xnPn+…)+(Eξ)2(P1+P2+…+Pn+…)=Eξ2—2(Eξ)2+(Eξ)2=Eξ2—(Eξ)2.
例4 设随机变量ξ的分布列为P(ξ=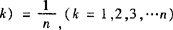 ,求Dξ.
,求Dξ.
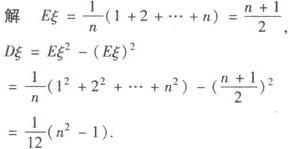
- 跨文化教育是什么意思
- 跨文化方法是什么意思
- 跨文化焦虑是什么意思
- 跨文化研究是什么意思
- 跨文化研究是什么意思
- 跨文化研究是什么意思
- 跨文化社会心理学是什么意思
- 跨时期价格歧视是什么意思
- 跨月份套利是什么意思
- 跨月份套利是什么意思
- 跨期套利是什么意思
- 跨期摊配帐户是什么意思
- 跨期节约是什么意思
- 跨期贸易是什么意思
- 跨栏跑是什么意思
- 跨民族的MMPI研究是什么意思
- 跨江击刘表是什么意思
- 跨河桥渡是什么意思
- 跨界交粮是什么意思
- 跨界语言是什么意思
- 跨省安置是什么意思
- 跨系统联行往来是什么意思
- 跨线设备是什么意思
- 跨绕是什么意思
- 跨膜电位是什么意思
- 跨膜离子流是什么意思
- 跨著是什么意思
- 跨虎势是什么意思
- 跨越与造就是什么意思
- 跨越世纪之梦是什么意思
- 跨越世纪的一代是什么意思
- 跨越人生障碍是什么意思
- 跨越卡夫丁峡谷是什么意思
- 跨越国界线是什么意思
- 跨越长度是什么意思
- 跨越长度原理是什么意思
- 跨越鸿沟是什么意思
- 跨距层次原则是什么意思
- 跨距长度测定法是什么意思
- 跨车是什么意思
- 跨车是什么意思
- 跨过 跨越是什么意思
- 跨过苏伊士运河是什么意思
- 跨运车是什么意思
- 跨部门的生产联系是什么意思
- 跨音速定常势流的混合差分法是什么意思
- 跨音速飞行是什么意思
- 跨鳌集是什么意思
- 跨鹤缠腰是什么意思
- 跪是什么意思
- 跪是什么意思
- 跪是什么意思
- 跪坐人是什么意思
- 跪坐俑是什么意思
- 跪坐弟子是什么意思
- 跪射武士俑是什么意思
- 跪拜是什么意思
- 跪石人辞是什么意思
- 跫然足音是什么意思
- 跫跫深径马蹄响,落落稀星著疏木。是什么意思