排队模型分类

---

排队论是研究排队现象的规律性，用以指导服务系统的最优设计和最优经营策略的数学分支，目前在企业生产经营中有广泛的应用。

排队模型是对排队现象的一种描述。排队系统模型种类很多，目前广泛采用的是Kendal1分类方法。

分类符号形式：

X／Y／Z

其中X处填写表示相继到达间隔时间的分布；

Y处填写表示服务时间的分布；

Z处填写并列的服务台的数目。

表示相继到达间隔时间和服务时间的各种分布的符号是：

M表示负指数分布或普阿松分布；D表示确定型；E_k表示k阶爱尔朗分布；G_I表示一般相互独立的随机分布；G表示一般随机分布。

其他几个符号：

μ表示单位时间能被服务完的顾客数(期望值)，称为平均服务率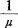；则表示一个顾客的平均服务时间；λ表示单位时间平均到达的顾客数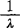；则表示相继顾客到达的平均间隔时间；ρ表示服务强度或称服务台的平均利用率，是刻划服务效率和服务机构利用程度的重要指标。