拉普拉斯变换

---

11．1．1 拉普拉斯变换及其反演公式

f(t)的拉普拉斯变换：

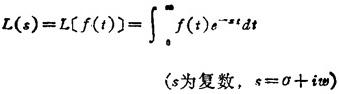
拉普拉斯变换的反演公式：

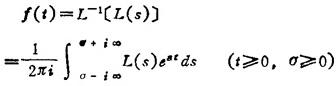
11．1．2 拉普拉斯变换的存在条件

如果f(i)满足下面三个条件，则它的拉普拉斯变换存在。

❶ 实变量的复值函数f(t)和f′(t)在t≥0上除掉有第一类间断点(在任意有限区间上至多有有限多个)外连续；

❷ 当t＜0时，f(t)=0；

❸ f(i)是有限阶的，即可以找到常数a≥0和A＞0，使得|f(t)|≤Ae^at(t≥0)。这里数a称为f(t)的增长指数，f(t)是有界函数时，可取a=0。11．1．3拉普拉斯变换的性质

L〔af〔t)〕=aL〔f(t)〕(a为常数)

L〔af(t)+bg(t)〕=aL〔f(t)〕+bL〔g(t)〕(a、b为常数)

L〔f(t)*g(t)〕=L〔f(t)〕·L〔g(t)〕

式中

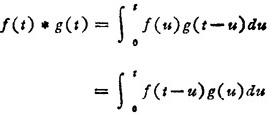
称为函数f(t)和g(i)的卷积(或褶积)。

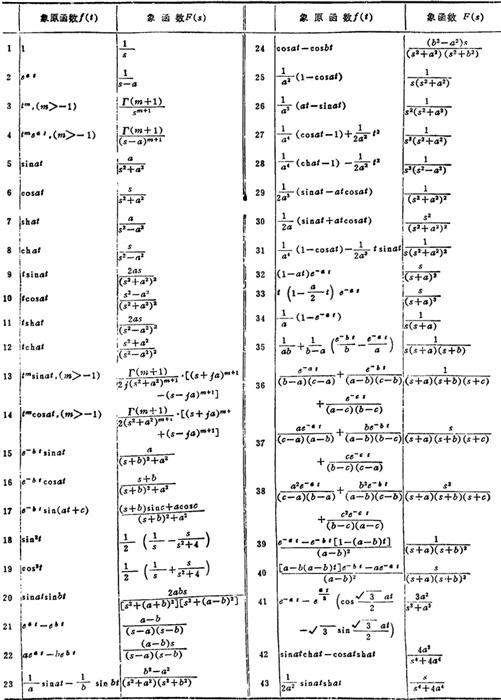
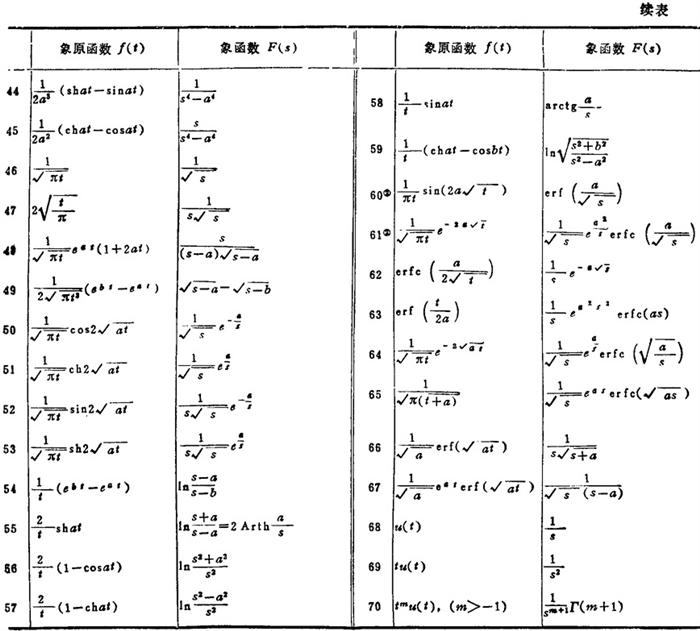
11．1．4 拉普拉斯变换简表

见表1．1－15。

表1．1－15 拉氏变换简表