广义矩法

---

广义矩估计法是参数估计的一种方法，是普通矩估计法的推广。

参数的矩估计就是用样本矩去估计总体矩。经常使用的是用样本一阶矩去估计总体一阶矩(均值)，用样本二阶中心矩去估计总体二阶中心矩(方差)。较成熟的GMM方法是由Hansen(1982)引进的，现在该方法已有较普遍的应用。

设ω_i是一个h×1的观测值向量，θ是a×1的未知参数向量，h(θ，ω_i)是一个r×1的向量函数，也就是

h(·)：(R^h×R^a)→R^r，R^h×R^a表示h×a实空间。

由于ω_i是随机的，所以h(θ，ω_i)也是随机的，假定当θ为参数真实值时

E[h(θ，ω_i)]=0 (1)

即函数h满足正交条件。记

y_n=(ω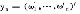，…，ω′_n)′ (2)

为样本观测值的全体集合，记

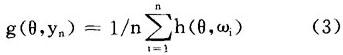
为函数h(θ，ω_i)的样本均值，g(·)是一个r维向量。

GMM基本思想是选择θ，使二次型

Q(θ，y_n)=[g(θ，y_n)]′W_n[g(θ，W_n)] (4)

取极小值。这里权函数矩阵W_n，n=1，2，…是一个r×r的矩阵序列。

为求θ的估计值，在(4)式中取权函数矩阵W_n的初值为单位阵，即Q为普通欧氏距离，使Q取极小而得到θ_n的初值θ_n⁽¹⁾。将θ_n⁽¹⁾代入

M_n=1／ng_n(X)[h(θ_n，ω_i)][h(θ_n，ω_i)]′ (5)

可得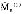_n⁽¹⁾，将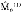_n⁽¹⁾代入

Q(θ，y_n)=[g(θ，y_n)]′M^－1[g(θ，y_n)] (6)

(其中M是h(θ，ω_i)的样本均值g(θ，y_n)的渐进方差，M^－1是M的逆矩阵)又可得θ_n⁽²⁾，如此迭代下去，直至‖θ_n⁽¹⁾－θ_n⁽ⁿ⁾‖小于预定精度ε为止。可以证明这个迭代过程与初值无关。