工具变量法

---

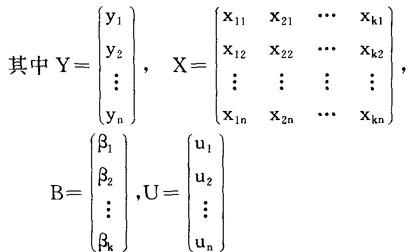
对于回归方程

y_1i=β₁x_1i+…+β_kx_ki+u_i

i=1，…，n (1)

其中解释变量的一部分是随机的，另一部分是确定性的。

由于随机的解释变量与随机干扰项相关，致使OLS法得到的参数估计不是一致估计。工具变量法是在这种情况下得到参数一致估计的常用方法。

希望能找到一些变量来替代方程右端中的随机解释变量，这些变量具有下列性质：
❶ 必须是外生变量，与结构方程中的随机扰动项不相关；
❷ 必须与将要替代的方程中的随机解释变量高度相关；
❸ 必须与已经出现在结构方程中作为解释变量的外生变量相关性极小以避免多重共线性；
❹ 引入的多个替代变量之间的相关性必须极小，以避免多重共线性。用这些变量去替代方程右端的随机解释变量，方程将满足OLS的应用假设条件。这些变量起了“工具”的作用，故名“工具变量法”。

将(1)表示为：

Y=XB+U (2)

因为解释变量中有随机变量，可应用工具变量法，选择工具变量Z代替X，用工具变量乘方程(2)两边：

Z′Y=Z′XB+Z′U

由于工具变量与随机干扰项不相关，因而Z′U为0，就得到工具变量法的参数估计

Z′Y=Z′XB

# (3)