导数的几何意义

---

曲线y=f(x)上任一点(x，y)的切线的斜率是f(x)在x处的导数，即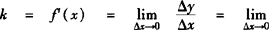 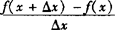，也就是说，曲线y=f(x)在点P(x₀，f(x₀))处的切线的斜率是f′(x₀)，相应地，切线方程为

y—y₀=f(x₀)(x—x₀)．

例1 利用导数的定义，求下列函数的导数．

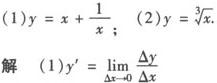
例2 证明 若函数f(x)在点x₀处可导，则f(x)在点x₀连续．

证明 要证f(x)在点x₀处连续，即证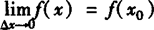于是只要证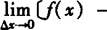：f(x₀)〕=0，而利用函数f(x)在点x₀处可导可以证明这一点．

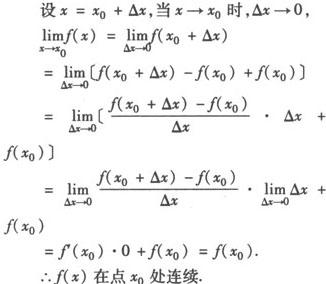
其逆命题：“若函数f(x)在点x₀处连续，则它在点x₀处可导”是否成立呢?回答是否定的，如函数y=|x|在点x=0处连续，但在点x=0处不可导，请读者自己给出证明．

例3 求证y=|x|在点x=0处连续，但在点x=0处不可导．

证明 只需证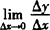不存在即可证明在x=0处不可导．

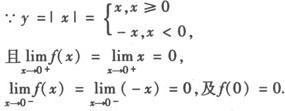
∴f(x)=|x|在点x=0连续．△y=f(0+△x)—f(0)=|△x|，